1. Геометрия
  2. Знайдіть висоту конуса, якщо

Знайдіть висоту конуса, якщо площа його основи дорівнює 27п см^2, а твірна нахилена до площини основи під кутом 30.

sevara17 sevara17    3   20.05.2019 19:10    2

Ответы
kazybekabdrahman0707 kazybekabdrahman0707  14.06.2020 07:03

Знайдемо радіус круга, що є основою конуса:
S = \pi r^2\\ \pi r^2 = 27\pi\\ r^2 = 27\\ r = \sqrt{27}=3\sqrt3\ (cm)\\
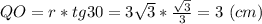
Розглянемо прямокутний трикутник AOQ (кут О прямий як кут між основою конуса та його висотою). tg<QAO = QO/AO, звідки
QO = АО*tg<QAO. Підставимо значення:
QO = r*tg30 = 3\sqrt{3} * \frac{\sqrt{3}}{3} = 3\ (cm)
Відповідь: 3 см

ПОКАЗАТЬ ОТВЕТЫ
olganedbaylova olganedbaylova  14.06.2020 07:03

Находим радиус основания конуса:

R=\sqrt{\frac{27\pi}{\pi}}=\sqrt{27}=3\sqrt3 см

Помня, что в прямоугольном треугольнике тангенсом угла называется отношение противолежащего катета к прилежащему, и зная tg30⁰=√3/3, находим высоту конуса h:

h=Rtg30^0=3\sqrt3\cdot\frac{\sqrt3}{3}=3 см

всі...

Ну і як "Краще рішення" не забудь зазначити, ОК?! .. ;))))

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
scumak399p07zdf scumak399p07zdf  20.10.2020 14:01
Точка L не лежить у ромбі ABCD. Доведіть що (LAB) || CD​...
timofeierofeev timofeierofeev  20.10.2020 14:02
Напиши уравнение окружности, которая проходит через точку 2 на оси Ox, и через точку 1 на оси Oy, если известно, что центр находится на оси Oy.  x^2+(y−?)^2=?^2.​...
Хаченок1337 Хаченок1337  11.12.2020 23:06
Хелп молю вас люди дорогре через 5 минут надо сдавать впссс​...
Новичок301117 Новичок301117  11.12.2020 23:06
Вертикальная башня высотой 35√3 м видна из точки К на поверхности земли под углом 600.Найдите расстояние от точки К до основания башни и до самой высокой точки башни.​...
9416451 9416451  11.12.2020 23:07
3. В равнобедренном треугольнике ABC с основанием BC = 28 см отрезок AD - бисcектриса, угол BAD = 36 см. Найдите CD, угол BAC, угол...
imaria1 imaria1  11.12.2020 23:09
Точка Е делит сторну ВС квадрата АВСD в отношении 2: 3, считая от точки В. Отрезки DЕ и АС пересекаются в точке О. Площадь треугольника СОЕ равна 18 см2. Найдите площадь треугольника...
КэтЗед КэтЗед  11.12.2020 23:10
3.[ ).Для острого угла найдите cosА  ,      tgА ,       ctgА, если известно, что sinА= 3.[ ).Для острого угла найдите cosА  ,      tgА ,       ctgА, если известно, что sinА=...
elyaivanova85 elyaivanova85  11.12.2020 23:10
Назовите выпуклый многогранник, у которого 6 вершин и 12 ребер.Сколько у него граней?...
virabasusta virabasusta  27.12.2020 09:08
. Любая высота любого треугольника равна данному треугольнику. делится на два треугольника?А) Равносторонний.Б) Любой.В) Равносторонний.Г) Такого треугольника нет.​...
gundinamaria gundinamaria  27.12.2020 09:10
Соч по геометрии 11 класс!(...

Популярные вопросы