Знайдіть площу ромба зі стороною 10 см, якщо сума його діагоналей дорівнює 28 см.

Дан ромб ABCD; AB=10см; AC+BD=28см.

Найти S(ABCD).

Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть AC∩BD=O.

AO+BO = AC:2+BD:2 = (AC+BD):2 = 28см:2 = 14см

ΔABO - прямоугольный (∠O=90°). Пусть AO=x см, тогда BO=14-х см

По теореме Пифагора:

AO²+BO² = AB² ⇒ x²+(14-x)²=100²

2x²-28x+96 = 0;   x²-14x+48 = 0;   x(x-8)-6(x-8) = 0;   (x-8)(x-6) = 0

x=6 или x=8

Если AO=6см, то ВО=8см, АС=12см, BD=16см

Если АО=8см, то ВО=6см, АС=16см, BD=12см

Получается ABCD это ромб с диагоналями, равными 16см и 12см.

Площадь ромба равна полупроизведению его диагоналей.

S(ABCD) =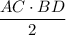 = 16·12:2 см² = 8·12 см² = 96см²

ответ: 96см².