. Знайдіть невідомі сторони і кути трикутника АВС, якщо: а) ВС = 6 см,

г) АС = 6 см, АВ = 8 см,

4. Під яким кутом видно прямолінійний край лісу АВ = 1240 м із пункту С, який віддалений від А на 1600 м і від В – на 1170 м (Мал. 6)?

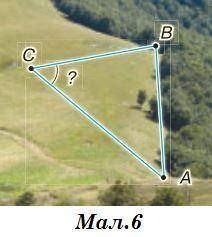
6. На Мал. 8 зображено дві прямі дороги KM і PN, які перетинаються десь за лісом у недоступній точці С. Потрібно знайти відстань від деякого пункту А на дорозі КМ до точки С перетину доріг. Для цього позначили на дорозі PN пункт В так, щоб можна було виміряти відстань АВ, і визначили кути ВАМ і ABN. Поясніть іб знаходження відстані АС. Обчисліть АС, якщо АВ = 800 м,

очень нужнооо

Добро пожаловать в урок геометрии! Давайте начнем с решения первого вопроса.

1. а) Зная, что ВС = 6 см, нам нужно найти остальные стороны и углы треугольника АВС. Для этого мы можем воспользоваться известными геометрическими правилами.

Для нахождения недостающих сторон и углов мы можем использовать теорему косинусов и теорему синусов. Давайте начнем с теоремы косинусов.

Теорема косинусов гласит, что квадрат длины одной из сторон треугольника равен сумме квадратов длин остальных двух сторон минус удвоенное произведение этих сторон на косинус соответствующего угла.

Для данного треугольника у нас есть сторона ВС = 6 см и мы хотим найти стороны АВ и АС. Давайте обозначим АВ = х и АС = у.

Используя теорему косинусов для стороны ВС, мы можем записать: 6^2 = х^2 + у^2 - 2ху * cos(∠BAC).

Второе уравнение, которое нам понадобится, - это теорема синусов. Она гласит, что отношение длины стороны треугольника к синусу противолежащего ей угла равно постоянной величине, равной удвоенному радиусу описанной окружности.

Используя теорему синусов для стороны ВС, мы можем записать: sin(∠BAC) = BC / AB.

Теперь у нас есть два уравнения с двумя неизвестными (х и у), и мы можем решить их систему для нахождения значений этих сторон.

2. г) В данном случае нам известны стороны АВ = 8 см и АС = 6 см и нам нужно найти остальные стороны и углы треугольника АВС.

Используя теорему косинусов и теорему синусов, мы можем снова составить систему уравнений и решить ее для нахождения недостающих значений.

Вы можете продолжить решение этой задачи самостоятельно, используя методы, которые я описал выше.

3. Для решения этого вопроса вам нужно использовать теорему косинусов. Давайте обозначим угол, под которым видно прямолинейный край леса, как ∠BAC и обозначим стороны треугольника АВС как АС = а, АВ = b и ВС = с.

Используя теорему косинусов для стороны АВ, мы можем записать: b^2 = а^2 + с^2 - 2ас * cos(∠BAC).

Теперь нам нужно найти угол ∠BAC. Для этого мы можем использовать теорему синусов. Она гласит, что отношение длины стороны треугольника к синусу противолежащего ей угла равно одному и тому же для всех сторон.

Используя теорему синусов для стороны АВ, мы можем записать: sin(∠BAC) = с / b.

Для решения этой задачи вам придется использовать углы и стороны, указанные на рисунке Мал. 6 и применить теорему синусов и косинусов.

4. Для решения этой задачи вам нужно использовать теорему косинусов и знание углов ВАМ и ABN.

Давайте обозначим стороны треугольника АВС как АВ = 800 м, АС = а и АВ = b.

Используя теорему косинусов для стороны АВ, мы можем записать: 800^2 = а^2 + b^2 - 2ab * cos(∠VAM).

Теперь мы должны использовать информацию об углах ВАМ и ABN, чтобы связать их с величиной ∠VAM и найти значение ∠VAM.

После нахождения значения ∠VAM, вы можете подставить его в первое уравнение и найти значение стороны АС.

Это были решения ваших задач. Учтите, что каждая задача может быть решена разными способами, и моя предложенная методика представляет только один из возможных подходов.