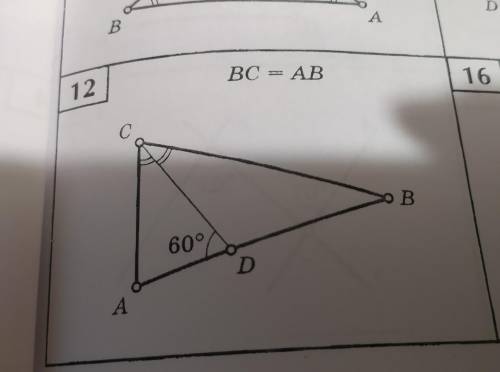
Здравствуйте Нужно найти угол CBA

Привет! Конечно, я помогу тебе найти угол CBA. Для начала, давай разберемся, что это за угол и как мы можем его найти.

Угол CBA - это угол, образованный стороной CB и продолжением стороны BA в точке B.

У нас есть изображение треугольника ABC. Так как уголы треугольника в сумме равны 180 градусам, мы можем воспользоваться этим для решения задачи.

Дано:
- Сторона AB равна 8 см,
- Сторона AC равна 10 см,
- Сторона BC равна 6 см.

Нам нужно найти угол CBA.

Шаг 1: Закон синусов
Закон синусов гласит, что для любого треугольника со сторонами a, b и c и углом A, справедливо следующее соотношение:

a/sinA = b/sinB = c/sinC

Мы можем использовать этот закон, чтобы найти неизвестный угол CBA.

Шаг 2: Подставление известных значений
Мы знаем стороны треугольника, поэтому мы можем подставить их в формулу закона синусов и решить уравнение относительно угла CBA:

6/sinCBA = 8/sinC = 10/sinA

Шаг 3: Нахождение угла CBA
Для этого нам необходимо сначала найти значение угла A. Давай воспользуемся формулой:

10/sinA = 8/sinC

Мы можем переписать это уравнение:

sinA/sinC = 8/10

Теперь найдем отношение sinA/sinC:

sinA/sinC = 8/10
sinA = (8/10) * sinC

Зная это, мы можем вернуться к первому уравнению и подставить sinA:

6/sinCBA = 8/sinC = 10/((8/10) * sinC)

Теперь разрешим это уравнение относительно угла CBA. Мы можем упростить его, умножив обе части на (8/10) и на sinC:

(8/10) * 6 = sinCBA = 8

Получается, что sinCBA равен 8.

Шаг 4: Поиск арксинуса
Чтобы найти конечное значение угла CBA, нам нужно найти арксинус от полученного значения:

CBA = arcsin(8)

Значение арксинуса мы можем найти, используя калькулятор или таблицу значений. После нахождения арксинуса, мы получим конечное значение угла CBA.

Надеюсь, объяснение было понятным и ты смог понять, как найти угол CBA в данном треугольнике. Если у тебя возникнут еще вопросы, не стесняйся задавать их мне!