Заранее если ответите правильно то подпишусь
Другие вопросы по теме Геометрия
Популярные вопросы
- , через несколько минут урок! Найдите на и больше значение ,,х,, в уравнении...
3 - Визначте які формули бінарних сполук складено не правильно....
3 - Замени слово ливень близким по значению...
1 - Чому дорівнює площа чотирикутника ABCD, що зображений в рисунку, якщо сторона...
1 - Почему нельзя изобразить на карте все, что есть на земном шаре?...
1 - Під час розчинення у хлоридній кислоті сплаву магнію з алюмінієм масою 50...
3 - 4. Указати складносурядне речення з єднальним сполучником : A Mине час,...
1 - Заспівувач хору називався …...
1 - БУДЬ ЛАСКА ДО ІТЬ. Обчисліть інтеграл...
2 - Укажіть пару елементів, які мають подібні хімічні властивості: а) Cl, Р; ...
3
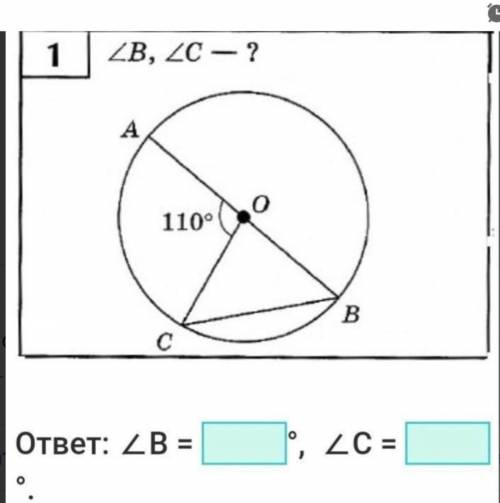
∠В = 55°; ∠С = 55°.
Объяснение:
1) Так как СО = ОВ как радиусы окружности, то ΔСОВ - равнобедренный, и углы при его основании равны между собой:
∠С = ∠В.
2) ∠АОС - внешний угол треугольника СОВ. Согласно теореме о внешнем угле треугольника, ∠АОС равен сумме двух других углов треугольника СОВ, не смежных с ∠АОС , то есть:
∠АОС = ∠С + ∠В.
Но так как ∠С = ∠В, то:
∠С = ∠В = 110° : 2 = 55°
ответ: ∠В = 55°; ∠С = 55°.