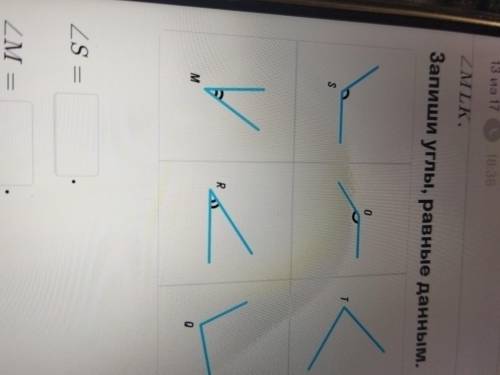
Запиши углы, равные данным. S У R 0 ZS — ZM =

Для того чтобы решить эту задачу, нам нужно определить все углы, которые равны углу между прямыми S и R.

В данной задаче мы имеем пересекающиеся прямые SR и ZS. Обозначим точку пересечения прямых SR и ZS как точку M.

Первым шагом мы можем определить значение угла ZSM. Для этого нам нужно заметить, что угол ZSM и угол ZSR (обозначенный как угол 0) являются вертикальными углами. Вертикальные углы имеют одинаковую меру, поэтому мы можем сказать, что угол ZSM равен углу 0.

Далее, мы можем использовать информацию о треугольниках ZSR и ZMS для определения значений других углов.

В треугольнике ZSR мы уже знаем, что угол ZSR (обозначенный как угол 0) равен углу ZSM. Также, угол RSZ (обозначенный как угол 1) является внутренним углом треугольника ZSR и его мера неизвестна.

Мы также знаем, что угол ZSM (обозначенный как угол 0) равен углу ZMS. Из этого следует, что угол SZM (обозначенный как угол 2) является внутренним углом треугольника ZMS и его мера неизвестна.

Теперь мы можем применить свойство треугольника, согласно которому сумма мер всех внутренних углов треугольника равна 180 градусов.

Применяя это свойство к треугольнику ZSR, мы можем записать следующее уравнение:
Угол 0 + Угол 1 + Угол 2 = 180

Так как угол 0 равен углу ZSM и угол 2 равен углу SZM, мы можем заменить эти значения в уравнении:
Угол ZSM + Угол 1 + Угол SZM = 180

Известно, что угол ZSM равен углу 0:
Угол 0 + Угол 1 + Угол SZM = 180

Теперь мы можем выразить угол 1 через уравнение:
Угол 1 = 180 - (Угол 0 + Угол SZM)

Угол 1 равен разности между 180 градусов и суммой мер углов 0 и SZM.

Таким образом, для того чтобы записать углы, равные данному углу, нам нужно записать:
1) Угол ZSM равен углу 0.
2) Угол 1 равен 180 - (Угол 0 + Угол SZM).

Надеюсь, что это объяснение помогло вам разобраться с задачей!