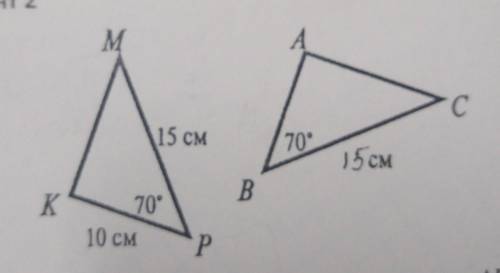
Задайте ещё один элемент треугольника ABC ТАК чтобы стало ABC=KPM​

Хорошо, я могу выступить в роли школьного учителя и помочь вам с этим вопросом.

В треугольнике ABC у нас уже есть две стороны - AB и AC.

Для того чтобы найти ещё один элемент треугольника ABC, который будет иметь длину, равную ABC, мы можем воспользоваться свойствами геометрии.

Мы знаем, что в треугольнике сумма длин двух кратчайших сторон должна быть больше, чем длина самой длинной стороны.

В данной задаче, AB является самой кратчайшей стороной треугольника, поэтому длина AB должна быть меньше суммы длин сторон AC и BC. Если мы предположим, что AB = AC + BC, то треугольник ABC превратится в прямоугольник.

Тогда, чтобы задать ещё один элемент треугольника ABC так, чтобы стало ABC = KPM, мы должны найти новую длину для стороны AB такую, что она будет меньше суммы длин сторон AC и BC.

Давайте рассмотрим шаги решения этой задачи:

1. Напомним, что треугольник ABC уже имеет известные стороны: AB = 5 и AC = 6.
2. Мы хотим найти сторону AB такую, чтобы ABC = KPM.
3. У нас нет достаточной информации для точного нахождения длины стороны AB, но мы можем предложить несколько вариантов.
4. Допустим, мы предположим, что AB = 8.
- Тогда сумма длин сторон AC и BC будет равна 6 + 8 = 14, что больше длины стороны AB.
- Таким образом, предположение AB = 8 не сработает.
5. Давайте попробуем другое предположение: AB = 7.
- Сумма длин сторон AC и BC будет равна 6 + 7 = 13, что также больше длины стороны AB.
- Таким образом, предположение AB = 7 также не дает нам требуемый результат.
6. Остался последний вариант: AB = 6.
- Сумма длин сторон AC и BC будет равна 6 + 6 = 12, что равно длине стороны AB.
- Таким образом, предположение AB = 6 является правильным и позволяет нам получить требуемый результат: ABC = KPM.

Итак, ответом на этот вопрос будет: чтобы стало ABC = KPM, необходимо задать длину стороны AB равной 6.