Задано точки A(1;6;4), B(3;2;5), C(0;—1;1), D(2;—5;2). Яке з наведених тверджень правильне?
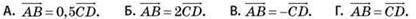
Другие вопросы по теме Геометрия
Популярные вопросы
- Определите самые популярные 3D-редакторы Ең танымал 3d редакторларын сәйкестендір...
1 - Айтылым 7 тапсырмаДиалогті толықтырындар.Әбділда Танабаевақын, ... ба?Иә, ол кісі...
2 - Задание 1 Прочитай стихотворение. Выпиши выделенные прилагательные. Объясни их...
3 - У МЕНЯ СОР 7 КЛАСС АЛГЕБРА ...
3 - 2. Рассмотрите рисунок рельефа дна океана и сопоставьте с формами рельефа на суше.Формы...
3 - РЕШИТЬ ЗАЧЕТ ПО ГЕОМЕТРИИ ЗА РАНИЕ...
1 - 1111111111111111111111111111...
2 - В ромбе одна из диагоналей равна 12 см а площадь этого ромба равна 48 квадратных...
3 - Укажите ряд слов, в котором только качественные прилагательные: таинственный шёпот,...
1 - Завдання 5. Скільки води, взятої при температурі 20°С, можна нагріти до температури...
1
1) Точка A(1;6;4) лежит в плоскости BCD.
Чтобы проверить это утверждение, мы можем использовать уравнение плоскости.
Уравнение плоскости можно записать в виде Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты, зная точки B, C и D.
Вычислим коэффициенты уравнения для плоскости BCD, используя точки B, C и D.
Из точки B(3;2;5):
3x + 2y + 5z + D = 0
Из точки C(0;-1;1):
0 + (-1) + z + D = 0
z - 1 + D = 0
Из точки D(2;-5;2):
2x + (-5)y + 2z + D = 0
Подставим значения из точек B и D в уравнение, используя переменные x, y и z из точки A:
3(1) + 2(6) + 5(4) + D = 0
3 + 12 + 20 + D = 0
35 + D = 0
D = -35
Подставим D = -35 в уравнение для точки C:
z - 1 - 35 = 0
z - 36 = 0
z = 36
Таким образом, уравнение плоскости BCD имеет вид:
3x + 2y + 5z - 35 = 0
Подставим значения x, y и z из точки A в это уравнение:
3(1) + 2(6) + 5(4) - 35 = 0
3 + 12 + 20 - 35 = 0
35 - 35 = 0
0 = 0
Так как левая часть уравнения равна правой, мы можем сделать вывод, что точка A(1;6;4) лежит в плоскости BCD.
Ответ: Утверждение "Точка A(1;6;4) лежит в плоскости BCD" правильное.
2) Точка B(3;2;5) принадлежит прямой AD.
Для проверки этого утверждения, мы должны найти вектор направления прямой AD и проверить, проходит ли точка B(3;2;5) через это направление.
Вектор направления прямой AD можно найти, вычитая координаты точек A и D:
AD = (2-1, -5-6, 2-4) = (1, -11, -2)
Теперь, чтобы проверить, проходит ли точка B через этот вектор направления, мы можем записать уравнение прямой в параметрической форме:
x = 1 + t
y = 6 - 11t
z = 4 - 2t
Подставим значения из точки B в эти уравнения:
3 = 1 + t
2 = 6 - 11t
5 = 4 - 2t
Из первого уравнения получим: t = 2.
Подставим t = 2 во второе и третье уравнения и проверим, выполняются ли они:
2 = 6 - 11(2)
2 = 6 - 22
2 = -16 (- не выполняется)
5 = 4 - 2(2)
5 = 4 - 4
5 = 0 (- не выполняется)
Таким образом, значения второго и третьего уравнений не выполняются, значит точка B(3;2;5) не принадлежит прямой AD.
Ответ: Утверждение "Точка B(3;2;5) принадлежит прямой AD" неправильное.
3) Прямая AD является перетином площин BCD і BDA.
Чтобы проверить это утверждение, мы можем найти направляющие векторы для плоскостей BCD и BDA.
Направляющие векторы для плоскости можно получить, используя векторное произведение двух векторов, лежащих в плоскости.
Для плоскости BCD возьмем векторы BC и BD:
BC = (0-3, -1-2, 1-5) = (-3, -3, -4)
BD = (2-0, -5-(-1), 2-1) = (2, -4, 1)
Теперь найдем их векторное произведение:
BCD = (-3, -3, -4) x (2, -4, 1) = ((-3)(1) - (-4)(-4), (-4)(2) - (-3)(1), (-3)(-4) - (-4)(2))
= (1 + 16, -8 + 3, 12 - 8) = (17, -5, 4)
Для плоскости BDA используем векторы BA и BD:
BA = (1-0, 6-(-1), 4-1) = (1, 7, 3)
BDA = (1, 7, 3) x (2, -4, 1) = ((1)(1) - 3(2), (3)(1) - (1)(2), (1)(-4) - (2)(7))
= (1 - 3, 3 - 2, -4 - 14) = (-2, 1, -18)
Теперь, чтобы проверить, перпендикулярна ли прямая AD обеим плоскостям BCD и BDA, мы можем найти скалярное произведение вектора направления AD и векторного произведения для каждой плоскости.
Если скалярное произведение равно нулю, то это означает, что вектор направления и векторное произведение перпендикулярны друг другу.
AD = (1-2, 6-(-5), 4-2) = (-1, 11, 2)
Скалярное произведение AD и BCD:
(-1, 11, 2) * (17, -5, 4) = (-1)(17) + (11)(-5) + (2)(4)
= -17 - 55 + 8 = -64 ≠ 0
Скалярное произведение AD и BDA:
(-1, 11, 2) * (-2, 1, -18) = (-1)(-2) + (11)(1) + (2)(-18)
= 2 + 11 - 36 = -23 ≠ 0
Таким образом, скалярные произведения AD и BCD, AD и BDA не равны нулю. Следовательно, прямая AD не является пересечением плоскостей BCD и BDA.
Ответ: Утверждение "Прямая AD является пересечением плоскостей BCD и BDA" неправильное.
Надеюсь, что это объяснение помогло вам понять, почему каждое утверждение правильное или неправильное. Если у вас есть еще вопросы, пожалуйста, задавайте!