Задание: В треугольнике ABC MN||AC.
Найдите x и y
Другие вопросы по теме Геометрия
Популярные вопросы
- 3. в российской федерации составляют 81,5 % всего населения. наше государство...
3 - Позначте рівняння реакції основи із сіллю: 1)2lioh+mgcl2=2licl+mg(oh)2...
3 - Уроки французского в краткой форме...
1 - Антоніми до слів: глибока, тихе.свіжий....
2 - Кросворд по биологии на тему эволюция,индивидуальное развитие,эволюция...
2 - Вдетстве александр суворов был ростом мал,тощ,плохо сложен и некрасив,вечно...
3 - Сочинение.если прийти в библиотеку ночью или просто внимательно прислушаться,можно...
3 - Написать сочинение по картине коровина зима ( 34 заранее огромное )...
2 - Нужен план 6 главы по робинзону крузо...
3 - Сумма всех чисел равна 30. одно из чисел в 1,5 раз больше чем другое. найдите...
1
Объяснение:
∆ВMN~∆АВС
Так как MN || AC, то MN отсекает от ∆АВС подобный ему ∆ВMN, поэтому соответствующие стороны этих треугольников пропорциональны. В каждой задаче будем рассматривать эти 2 треугольника.
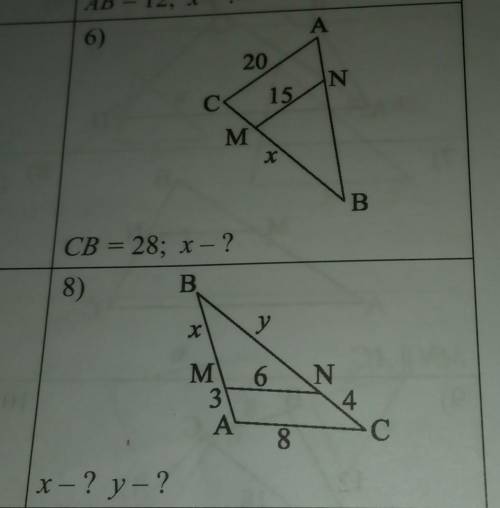
№6
Составим пропорцию:
MN/АС=х/СВ
Перемножим крест накрест:
АС×Х=MN×СВ
20х=15×28
20х=420
х=420÷20
х=21
ОТВЕТ: х=21
№7
Пусть АВ=3+х, пропорция:
MN/АС=х/АВ
АС×Х=MN×АВ
8х=6×(х+3)
8х=6х+18
8х–6х=18
2х=18
х=18÷2
х=9
Пусть ВС=4+у, пропорция:
MN/АС=у/ВС
АС×у=MN×ВС
8у=6×(4+у)
8у=24+6у
8у–6у=24
2у=24
у=24÷2
у=12
ОТВЕТ: х=9, у=12