Задана прямая общими уравнениями и координаты двух точек. Необходимо: 1) написать канонические уравнения прямых; 2) найти угол
между прямыми.
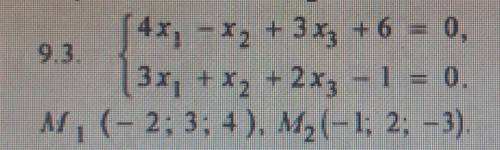
Другие вопросы по теме Геометрия
Популярные вопросы
- 7,5×0,0204; 0,008×2,2; 10,2×0,055покажите в тетради...
3 - Рассмотрите следующие положения: 1) Кто конфликтует (участники...
3 - Как решить 12+у=48 уравнения...
2 - 7 тапсырма . Үш нұсқаның ішінен қажетті сөзді таңдап жаз ....
2 - 8. выполни действия:а)5 5/9-8/9;б)7 11/12+4 5/12;в)8-5 5/7;г...
1 - Как могу проявляться выразительные возможности гармонии?...
1 - Скласти твір Поліанна дарує радість...
2 - сделать план Якуб колас у старых дубах...
3 - 1 со знаменателем и большую 210 Запишите дробь, равную а) 10;...
3 - Памагите завтра здавать 9 класс Докажите, что при всех доступных...
3
1) Написание канонических уравнений прямых:
Для того чтобы написать каноническое уравнение прямой, нам понадобятся две вещи: угловой коэффициент (наклон) прямой и точка, через которую она проходит.
Угловой коэффициент (k) можно найти, используя координаты двух точек на прямой (x1, y1) и (x2, y2) с помощью формулы:
k = (y2 - y1) / (x2 - x1)
Далее, мы можем выбрать любую из этих точек и подставить ее координаты в уравнение прямой вида y = kx + b, чтобы найти значение пересечения с осью y (b).
Теперь мы можем записать каноническое уравнение прямой вида Ax + By + C = 0, где A, B и C - это определенные числа, не зависящие от наклона прямой, а только от координат и уравнений параллельных и перпендикулярных прямых. Чтобы получить их значения для нашей прямой, мы можем использовать следующие формулы:
A = -k
B = 1
C = -b
Теперь у нас есть каноническое уравнение прямой!
2) Нахождение угла между прямыми:
Чтобы найти угол между прямыми, нам нужно знать их угловые коэффициенты. Для заданных канонических уравнений прямых, угловые коэффициенты будут обратными числами коэффициентов перед x.
Для первой прямой, угловой коэффициент равен 1/3, а для второй прямой он равен -1/2.
Теперь, чтобы найти угол между прямыми, мы можем использовать следующую формулу:
угол = arctan(|(k2 - k1) / (1 + k1 * k2)|)
где k1 и k2 - угловые коэффициенты первой и второй прямых соответственно.
Используя эту формулу и подставляя значения угловых коэффициентов, мы можем найти угол между прямыми.
И это все! Я надеюсь, что мой ответ был понятным и полезным для тебя. Если у тебя есть еще вопросы, не стесняйся спрашивать!