Задача на нахождение угла треугольника , с объяснением )
Другие вопросы по теме Геометрия
Популярные вопросы
- Отметьте города где перерабатывают нефтепродуктыотметьте города где перерабатывают...
3 - 724. өрнекті жазып алып, ықшамдаңдар: 1) псанынан басталған тізбектес үш натурал...
1 - Как определить наличие кислоты в продуктах питания в условиях?...
3 - Вводится число n^k . определить есть ли цифра m в числе...
1 - По ! периметр равнобедренного треугольника = 48 см.его стороны относятся как...
2 - Перевести числа из десятичной системы счисления сначала в двоичную систему,...
2 - ответьте на вопросы. желательно не много писать ещё...
3 - Пылинка с зарядом -0,35 нкл приближается к пылинке с зарядом +1,2нкл на каком...
3 - Составить текст поздравления с новым годом, используя не менее 5 наречий с...
3 - Расставь по порядку действия,которые необходимо выполнить при размножении...
2
Відповідь:
10°
Пояснення:
∠А=180°-(∠В+∠С)=180°-90°=90°
АN - биссектриса, по условию задачи
∠NAB=45°
∠ВNA=180°-(55°+45°)=80°
рассмотрим ΔNAН, он прямоугольний и ∠ВNA=80° →
∠NAН=90°-∠ВNA=90°-80°=10°
Відповідь:
НАN = 10°
Пояснення:
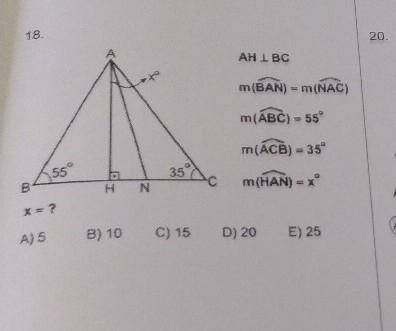
Дан треугольник АВС, АН - высота ( угол ВАN = NАС ) , АN - биссектриса ( угол АНС - прямой ). Найти угол НАN.
Угол НАС = 180 - 90 - 35 = 55°
Угол ВАС = 180 - 55 - 35 = 90°
Угол NАС = ВАС / 2 = 90 / 2 = 45°
Угол НАN = НАС - NАС = 55 - 45 = 10°