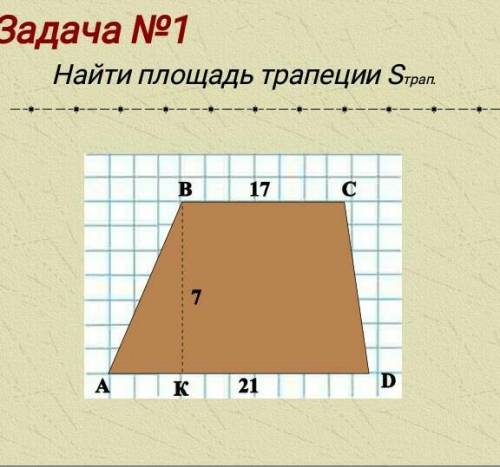
Задача 1 найдите площадь трапеции Sтрап.
Другие вопросы по теме Геометрия
Популярные вопросы
- Запеши в виде не правельнлй дроби 7 2/9; 5 8/17; 12 17/48 взяв...
1 - How many people visit Rome every year? What happened in the Colosseum?How...
1 - Сөйлемдерді мөлшер үстеулерімен /наречия меры/ толықтырып жаз....
3 - Учащиеся заполняют таблицу (раздаточый материал): Место в обществе...
3 - Преаброзуйте выражение(3x-4y)2...
1 - вопроса 1. Какую роль у турбеллярии играют мерцательные реснички,...
3 - Когда появились стрелки на брюках? Стрелки на брюках появились...
2 - «Жүзу спорты» тақырыбында сұхбат құрастыр....
3 - Анализ эпизодов и характеристика героев рассказа В.П. Астафьева...
2 - З яким максимальним прискоренням можна піднімати на мотузці тіло...
1
Чтобы найти площадь трапеции, нам понадобятся некоторые формулы и понимание, как работать с ними.
В данной задаче у нас имеется трапеция, которая представлена на картинке. Нужно найти ее площадь Sтрап.
Трапеция - это четырехугольник, у которого две стороны параллельны, а другие две - нет. Для нахождения площади трапеции, можно воспользоваться следующей формулой:
Sтрап = ((a + b) * h) / 2,
где a и b - длины двух параллельных сторон трапеции, а h - высота трапеции, которая является перпендикулярной отрезку, соединяющему параллельные стороны и проходящему через их общую вершину.
Применим эту формулу для решения данной задачи. Но сначала найдем значения a, b и h.
На рисунке даны следующие значения сторон:
a = 12 см,
b = 6 см,
а высота h не указана. Но мы можем ее найти, используя информацию о прямых углах.
Для начала, посмотри на картинку внимательно. Ты видишь, что вертикальный отрезок высоты трапеции разделяет ее на два треугольника. Также заметь, что единственный угол на верхней границе одного из этих треугольников является прямым углом.
Зная это, мы можем использовать теорему Пифагора для вычисления высоты треугольника.
Теорема Пифагора утверждает, что для прямоугольного треугольника с катетами a и b и гипотенузой c выполняется следующее равенство:
c^2 = a^2 + b^2.
Мы можем применить эту формулу для нашего треугольника, где стороны a и b - это одна сторона трапеции и ее высота, а гипотенуза c - это диагональ трапеции.
По рисунку, мы можем видеть, что диагональ трапеции разделяет ее на два прямоугольных треугольника. Применив теорему Пифагора к этим треугольникам, мы найдем высоту h.
Давай начнем с прямоугольного треугольника слева. В этом треугольнике стороны a и b это 6 см и h (высота трапеции), а гипотенуза c - это одна из сторон трапеции.
Применим теорему Пифагора:
c^2 = a^2 + b^2,
c^2 = 6^2 + h^2.
Раскроем скобки и упростим:
c^2 = 36 + h^2.
Теперь посмотрим на прямоугольный треугольник справа. В этом треугольнике стороны a и b это 12 см и h (высота трапеции), а гипотенуза c - это другая сторона трапеции.
Применим теорему Пифагора:
c^2 = a^2 + b^2,
c^2 = 12^2 + h^2.
Раскроем скобки и упростим:
c^2 = 144 + h^2.
Теперь мы имеем два уравнения: c^2 = 36 + h^2 и c^2 = 144 + h^2. Оба уравнения равны c^2, так как используются одна и та же диагональ трапеции.
Сравним эти два уравнения:
36 + h^2 = 144 + h^2.
Здесь h^2 сокращается и остается:
36 = 144.
Это ложное уравнение, так как 36 не равно 144. Значит, решения нет.
Возможно, в задаче допущена ошибка, поскольку нельзя построить трапецию с указанными размерами. Если бы была дана другая высота или другие стороны, мы могли бы решить задачу и найти площадь трапеции по формуле Sтрап = ((a + b) * h) / 2.
Если у тебя остались вопросы, не стесняйся задавать их! Желаю удачи в изучении математики!