ЗА ПОДРОБНОЕ РЕШЕНИЕМ С ОБЪЯСНЕНИЕМ В треугольнике ABC, AM=MB,
BN=NC и MN+AC=24 см.
Найдите сторону AC.
ответы:
А) 8 см
B) 16 см
C) 18 см
D) 9 см
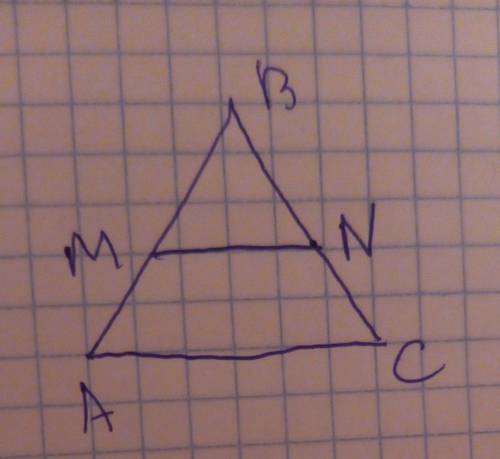
Другие вопросы по теме Геометрия
Популярные вопросы
- 4. Стала радіоактивного розладу Плутонік-239 дорівнює 9,01*10:13....
1 - Дайте полный ответ на вопрос: Нужно ли развивать искусство икебаны...
1 - 1)Почему сегодня наблюдается низкая ответственность родителей...
2 - 2 Cұраққа жауап беру арқылы мәтіннің негізгі ойын анықтаңыз....
2 - составить уравнения, указать механизм реакций, назвать продукты:...
1 - . «Автормен сырласу» ойыны. Фантаст-жазушы СахиевЖүнісне фантастика...
1 - Как устанавливается Игла в иглодержатель?...
3 - Даны координаты вершин пирамиды А1А2А3А4. Средствами векторной...
3 - Существует ли единороги? приведите факты...
2 - Реакция живых организмов на раздражители...
1
ответ: АС=16 см .
Так как АМ=МВ , то точка М - середина стороны АВ . Аналогично , из равенства BN=NC следует, что N - cередина стороны ВС .
Значит, MN - средняя линия треугольника .
По свойствам средней линии треугольника MN || AC и MN=1/2 * AC , то есть MN - половина стороны АС . Значит, АС=2* MN .
MN+AC=MN+2*MN=3*MN , 3*MN=24 cм ⇒ MN=24:3 , MN=8 см .
АС=2*MN=2*8=16 cм .
Объяснение:
MN - средняя линия треугольника АВС. MN=AC/2;
AC/2+AC=24
3AC=48
AC=48/3=16 см.