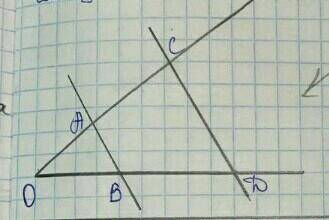
За данним рисунком AB||CD, OB=5, BD=7.Знайдіть відрізки OA і AC,якщо AC-OA=1
Другие вопросы по теме Геометрия
Популярные вопросы
- Работа с текстом . Прочитайте. О чем вы узнали? Найдите ключевые слова...
1 - 135,2 * 2,1 – ( 0, 083 + 0, 841) : 2,31...
3 - Подготовить письменное выступление на одну из предложенных тем:(8-10...
3 - 3-тапсырма Шығармадағы басты кейіпкерге мінездеме беріңіз.КейіпкерЖетім...
2 - 1. При каком значении b уравнения будут равносильными: 3х – 7 = 2...
1 - Найдите угловой коэффициент касательной, проведенной в точке x =1...
1 - обработки травм. Обж 9 класс ...
1 - Қазақ халқының балаға қатысты салт-дәстүрлерінің маңызы неде? Балаға...
2 - Постройте график функции у=2(х-2)2.найдите нули функции...
2 - Решите Дана функция: y = -х3 + 4х – 3 а) запишите координаты вершины...
2
Из условия задачи мы знаем, что AB || CD. Это означает, что угол AOB и угол COD являются соответственными углами и равны между собой.
Мы также знаем, что OB = 5 и BD = 7. Давайте воспользуемся этой информацией для нахождения длин отрезков OA и AC.
Первым шагом найдем длину отрезка OD. Мы можем найти его, используя теорему Пифагора для прямоугольного треугольника OBD:
OD^2 = OB^2 + BD^2
OD^2 = 5^2 + 7^2
OD^2 = 25 + 49
OD^2 = 74
Теперь найдем длину отрезка OC. Мы знаем, что AC - OA = 1, поэтому давайте представим отрезок OC как сумму отрезков OA и AC:
OC = OA + AC
Теперь мы можем записать уравнение с помощью информации из задачи:
AC - OA = 1
Также мы знаем, что отрезок AC делит отрезок OD в пропорции. Это означает, что отношение отрезка AC к отрезку OD равно отношению отрезка AB к отрезку OD:
AC / OD = AB / OD
Теперь мы можем записать уравнение, используя известные значения:
AC / sqrt(74) = 15 / sqrt(74)
Мы можем решить это уравнение, умножив обе стороны на sqrt(74):
AC = 15
Теперь, снова используя уравнение AC = OA + 1, мы можем найти значение отрезка OA:
OA = AC - 1
OA = 15 - 1
OA = 14
Итак, длины отрезков OA и AC равны соответственно 14 и 15.