1. Геометрия
  2. за 1 задачу Основа рівнобедреного

за 1 задачу Основа рівнобедреного трикутника дорівнює 10 см, а медіана, проведена до бічної сторони, -8 см. Знайдіть бічну сторону трикутника.

VadimButs VadimButs    1   19.12.2020 12:35    4

Ответы
dimar3256 dimar3256  18.01.2021 12:35

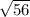AB = AC = \sqrt{56} см

Объяснение:

Дано:

AC = AB, BC = 10 см, BM = 8 см, CM = MA

Знайти:  AC,AB - ?

Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =

= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в

точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.

BM = BO + MO;

8 = 2y + y;

8 = 3y;

y =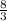 \frac{8}{3}  ;

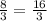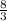BO = 2y = 2 * \frac{8}{3} = \frac{16}{3} ; MO = y = \frac{8}{3} ;

За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: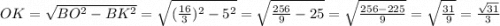OK = \sqrt{BO^{2} - BK^{2} }=\sqrt{(\frac{16}{3} )^{2} - 5^{2} }=\sqrt{\frac{256}{9} - 25}=\sqrt{\frac{256 - 225}{9} }=\sqrt{\frac{31}{9} }=\frac{\sqrt{31} }{3} ;

Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.

AK = OK + AO;

AK = x + 2x = 3x = 3*OK 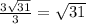 = \frac{3\sqrt{31} }{3} = \sqrt{31} ;

За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:

AB = \sqrt{KA^{2} +KB^{2} }=\sqrt{(\sqrt{31} )^{2} +5^{2} } =\sqrt{31 + 25}=\sqrt{56}

Так як AB = BC за умовою, то AB = AC =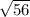 \sqrt{56} см.


за 1 задачу Основа рівнобедреного трикутника дорівнює 10 см, а медіана, проведена до бічної сторони,
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
мрамар мрамар  20.07.2019 15:40
Сn- биссектриса равнобедренного треугольника авс с основанием ас.найдите углы треугольника авс, если угол cnb=102 градуса...
Owlysoulowl Owlysoulowl  20.07.2019 15:40
Две стороны треугольника равны 5 в корне 3 и 6 см, а высота, проведённые к этим сторонам, пересекаются под углом 60 градусов. найдите площадь треугольника....
даряя1 даряя1  20.07.2019 15:40
Площадь прямоугольника равна 15,найдите его большую сторону,если она на 2 больше меньшей стороны...
natalyiphonep0725u natalyiphonep0725u  20.07.2019 15:40
Ао биссектриса угла а. найдите градусные меры острых углов треуг. авс. угол воа 109 гр, угол с прямой, вао=оас...
ника2346олл ника2346олл  06.10.2019 10:00
Ав кесіндісінің ұштары шамасы 60°қа тең екіжакты бұрыштың жақтарына тірелген. екіжакты бұрыштың қырына а және в нүктелерінен ad және вс перпендикуляр жүргізілген....
ПолинаПадафет15 ПолинаПадафет15  06.10.2019 10:00
Дано: abcd четырехугольник, ac пересекается с bd=0,oc=5см,ob=6см,oa=15см,od=18с. доказать bc параллельно ad.найти площадь aod деленную на площадь aob. скажите...
dimapoddubny20p08hrm dimapoddubny20p08hrm  06.10.2019 10:00
Радиус окружности, вписанной в правильный четырёхугольник, равен 2√2 см. вычеслить: а) его периметр б) диаметр окружности, описанной около четырёхугольника...
vika14112006 vika14112006  06.10.2019 09:50
Каково взаимное расположение при параллельном переносе: а)отрезка и его образа; б) луча и его образа; в)прямой и ее образа...
WseNikiZanyati WseNikiZanyati  06.10.2019 09:50
Відрізок ав і сд перетинаються в точці о, причому ао = во, со = до. знайдіть кут вдс і ас, якщо дса- 70 градусів. потрібно швидко....
Тупойшкольник0 Тупойшкольник0  15.05.2019 10:51
Т__т 1.знайти r для правильного чотирикутника, якщо a=6. 2.знайти довжину кола, якщо радіус дорівнює 7 см. 3.різниця між двома сторонами трикутника дорівнює 5 см,...

Популярные вопросы