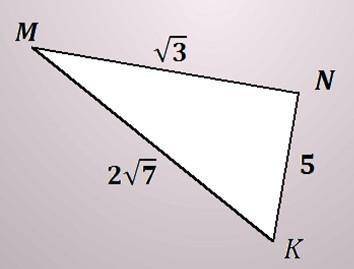
Является ли треугольник MNK прямоугольным?
!

Чтобы определить, является ли треугольник MNK прямоугольным, нужно обратить внимание на его стороны и углы. Для этого воспользуемся теоремой Пифагора и определим длины сторон треугольника. Для начала, нам понадобятся координаты точек M, N и K. По изображению видно, что точки M(1,2), N(4,6) и K(1,6). Теперь мы можем определить длины сторон треугольника. Для этого воспользуемся формулой для расстояния между двумя точками в декартовой системе координат: Для стороны MN: MN = sqrt((x2 - x1)^2 + (y2 - y1)^2) MN = sqrt((4 - 1)^2 + (6 - 2)^2) MN = sqrt(3^2 + 4^2) MN = sqrt(9 + 16) MN = sqrt(25) MN = 5 Для стороны NK: NK = sqrt((x2 - x1)^2 + (y2 - y1)^2) NK = sqrt((1 - 4)^2 + (6 - 6)^2) NK = sqrt((-3)^2 + (0)^2) NK = sqrt(9 + 0) NK = sqrt(9) NK = 3 Для стороны KM: KM = sqrt((x2 - x1)^2 + (y2 - y1)^2) KM = sqrt((1 - 1)^2 + (6 - 2)^2) KM = sqrt((0)^2 + (4)^2) KM = sqrt(0 + 16) KM = sqrt(16) KM = 4 Теперь у нас есть длины всех сторон треугольника. Чтобы определить, является ли треугольник прямоугольным, нужно проверить, выполняется ли теорема Пифагора: В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Если это утверждение верно для нашего треугольника, то треугольник MNK является прямоугольным. Для треугольника MNK: MN^2 = NK^2 + KM^2 5^2 = 3^2 + 4^2 25 = 9 + 16 25 = 25 Уравнение верно, так как обе стороны равны. Значит, треугольник MNK является прямоугольным. Таким образом, ответ на вопрос "Является ли треугольник MNK прямоугольным?" - да, треугольник MNK является прямоугольным.