Высота правильной треугольной пирамиды равна 2, а двугранный угол при основании 45°. Найдите площадь боковой поверхности пирамиды S. В ответ запишите S/корень из 6. С решением, будьте любезны
Другие вопросы по теме Геометрия
Популярные вопросы
- Од друга означает выражениеЧто«НОГИслуш1 -- 10достигстремлюсьухватил...
3 - Какой вклад внесли новотеченцы в развитие культуры и образования...
2 - Какая скорость токсичного действия у сероводорода? 1) АХОВ быстрого...
3 - Краткий анализ стихотворения тучи Лермонтов 6 класс очень краткий,...
2 - In teams make sentences. Use words from the list. Each correct...
2 - составить задачу по таблице и решить её♥️...
2 - Составить три вопроса по 1 и 2 параграфу. 7 класс всемирная история....
1 - 2 23 Listen again and write a word or number to complete the sentences....
1 - Физика, задание 2, на скришноте...
2 - 10 слов в родительном падеже из сказки Иван-крестьянский сын и...
3
Sбок=(Pосн*h)/2
1) ΔМОК: ∠О=90°, ∠К=45° ⇒ ∠М=45°
МО=ОК=2
МК=2√2=h апофема
2) КО=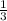 КС
КС
2 = 1/3 КС ⇒ КС = 6 - медиана в ΔАВС
3) m= (a√3)/2=6
а = (6*2)/√3
а=(12*√3)/3 = 4√3 ( сторона основания ΔАВС )
4) Sбок=(3*4√3*2√2)/2=12√6
ответ: S/√6=12√6/√6=12