1. Геометрия
  2. Высота правильногоо треугольника

Высота правильногоо треугольника равна 6 корней из трёх.найдите площадь круга описанного около треугольника

Laura11111111111 Laura11111111111    2   17.03.2019 08:30    2

Ответы
вика87 вика87  07.06.2020 03:10

Высота правильного треугольника равна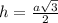 h=\frac{a\sqrt{3}}{2}

 

Сторона правильного треугольника равна

a=\frac{2\sqrt{3}h}{3};a=\frac{2\sqrt{3}*6\sqrt{3}}{3}=12;

 

Радиус описанной окружности равен

R=\frac{a\sqrt{3}}{3};R=\frac{12\sqrt{3}}{3}=4\sqrt{3}

 

Площадь круга описанного около треугольника равна

S=\pi *R^2; S=\pi*(4\sqrt{3}})^2=48 \pi

ПОКАЗАТЬ ОТВЕТЫ
pogosanitka2345 pogosanitka2345  07.06.2020 03:10

Т.к. высоту правильного треугольника можем узнать по формуле 

h=a*sqrt3/2, где a - сторона треугольника, то в данном случае:

a=2h/sqrt3=12sqrt3/sqrt3=12

Площадь правильного треугольника=a^2sqrt3/4, т.е. в нашем случае: S=144sqrt3/4=36sqrt3

R=abc/4S=12*12*12/144sqrt3=12/sqrt3=12sqrt3/3=4sqrt3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
andrei822 andrei822  09.08.2019 12:30
Вравнобокой трапеции диагонали перпендикулярны, высота равна 7см, периметр равен 30см. найдите боковую сторону трапеции...
adweafd adweafd  09.08.2019 12:30
Найдите площадь кругового сектора если градусная мера его дуги равна 20 градусов а радиус круга 3 сантиметров...
Котенька0209 Котенька0209  09.08.2019 12:30
1) у чотирикутнику авсd проведено дiагональ bd, угол сbd=углу adb, угол abd=углу bdc. довести що, abcd 2) одна з сторiн прямокутника у 5 разiв бiльша за другу. р=36см....
YTO4KA1337 YTO4KA1337  09.08.2019 12:30
Впрямоугольном треугольнике катет равен 12, а гипотенуза - 13. найти квадрат длины биссектрисы треугольника, проведенной из вершины меньшего угла...
maximkolosov66 maximkolosov66  09.08.2019 12:30
Окружность радиуса 1 вписана в угол величиной 60o. далее вписаны еще 62 окружности. при этом, окружность касается (для от 2 до 63). известно, что никакие две окружности...
egorbychkov83 egorbychkov83  09.08.2019 12:30
Гіпотенуза прямокутного трикутника дорівнює 10 см. якою найбільшою може бути площа трикутника?...
izeddin2002 izeddin2002  09.08.2019 12:30
Луч m проходит между сторонами угла (bc).найдите угол (bm) и угол (cm) если угол (bc)-75° угол (bm) в 4 раза меньше чем угол (cm)...
1234567890824 1234567890824  09.08.2019 12:30
Докажите что треугольник авс прямоугольный если а(-3; 2; 1), в(1; 1; 2), с(7; 20; -3; )...
sashaShelsy sashaShelsy  27.08.2019 19:10
Вравнобедренном треугольнике abc, угол b = 104 градуса, ad - высота. найти угол dac...
kadalsu4 kadalsu4  27.08.2019 19:10
Вравнобедренном треугольнике abc с основанием ac отрезок be - высота. найдите угол ebc, если ac =12 см и угол abc =74°...

Популярные вопросы