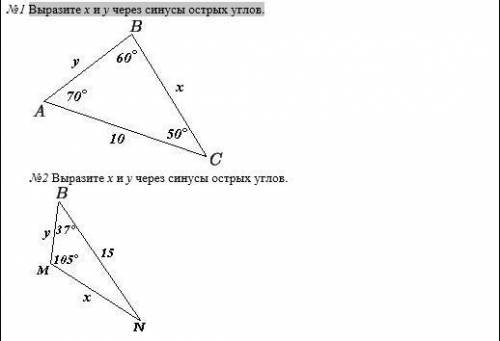
Выразите х и у через синусы острых углов.

Объяснение:

bzjzznbzjzkansbzjzs s

bmbhnxnzhhsjsjsbzjzkddn mznzjzkzjnznzjsnsnz s

bzjzkznzbnxmznznxjxmx.z mznzhzzjznzjmzjzjz.z s

Задача состоит в том, чтобы выразить значения переменных x и y в терминах синусов острых углов в данном треугольнике.

Перед тем, как ответить на вопрос, необходимо разобраться с основным свойством синуса в прямоугольных треугольниках. Согласно этому свойству, синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. Также, в данной задаче, мы имеем дело с тремя острыми углами, поэтому выразим синусы для каждого из них.

Обозначим sin(α) как синус острого угла α, где α - угол ACB, sin(β) - синус острого угла β, где β - угол CAB, и sin(γ) - синус острого угла γ, где γ - угол ABC.

Согласно свойству синуса, у нас есть следующие равенства:
sin(α) = AB/AC,
sin(β) = BC/AC,
sin(γ) = AB/BC.

Теперь мы можем выразить значения переменных x и y через sin(α), sin(β) и sin(γ).

1. Для выражения переменной x:
Из рисунка видно, что AC является гипотенузой прямоугольного треугольника ABC. Используя свойство синуса для угла β, получаем:
sin(β) = BC/AC.
Отсюда:
BC = sin(β) * AC.

Также, по теореме Пифагора имеем:
AB = sqrt(AC^2 - BC^2).

Следовательно:
AB = sqrt(AC^2 - (sin(β))^2 * AC^2) = sqrt(AC^2(1 - (sin(β))^2)) = AC * sqrt(1 - (sin(β))^2).

Таким образом, мы получаем:
x = AB = AC * sqrt(1 - (sin(β))^2) = AC * sqrt(1 - (BC/AC)^2) = AC * sqrt(1 - (sin(β))^2).

2. Для выражения переменной y:
Из рисунка видно, что AC является гипотенузой прямоугольного треугольника ABC. Используя свойство синуса для угла α, получаем:
sin(α) = AB/AC.
Отсюда:
AB = sin(α) * AC.

Также, по теореме Пифагора имеем:
BC = sqrt(AC^2 - AB^2).

Следовательно:
BC = sqrt(AC^2 - (sin(α))^2 * AC^2) = sqrt(AC^2(1 - (sin(α))^2)) = AC * sqrt(1 - (sin(α))^2).

Таким образом, мы получаем:
y = BC = AC * sqrt(1 - (sin(α))^2).

Таким образом, полные выражения для переменных x и y через синусы острых углов в терминах данной задачи следующие:
x = AC * sqrt(1 - (sin(β))^2),
y = AC * sqrt(1 - (sin(α))^2).

Важно помнить, что это только одно из множества возможных решений задачи. Зависимости между переменными и синусами углов могут быть разными в разных треугольниках.