выполните задания за правельный ответ​

14,4

Объяснение:

так правильно

Плоскость α , параллельная стороне АМ ΔАМD, пересекает его стороны DA и DM в точках К и Т соответственно. Найти отрезок ТК, если ТМ: МD=2: 5 , АМ=14 см

Объяснение:

Т.к. АМ║α, то линия пересечения  КТ плоскости (АМD)  и  α будет параллельна АМ.

ΔDКТ подобен ΔDAM по двум углам : ∠D-общий ,∠DKT=DAM как соответственные , DM-секущая ⇒ сходственные стороны пропорциональны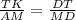   , на отрезок МD приходится 5 частей , на отрезок DT приходится 5-2=3 части.

 , ТК=8,4 см