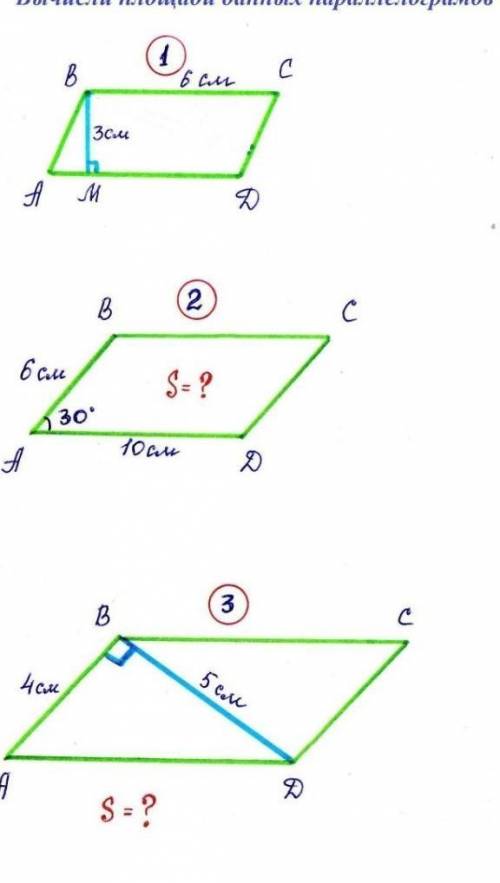
Вычислите площади данных параллелограмма​

Для вычисления площади параллелограмма нам необходимо знать его высоту и длину одной из сторон. В данном случае высота параллелограмма уже дана - она равна 6 см. Однако, нам необходимо вычислить длину стороны.

Для этого мы можем использовать теорему Пифагора. В треугольнике ABC прямая AC является высотой параллелограмма, а стороны AB и AC являются катетами. Зная, что AC = 6 см и BC = 10 см, мы можем применить теорему Пифагора:

AB^2 = AC^2 - BC^2
AB^2 = 6^2 - 10^2
AB^2 = 36 - 100
AB^2 = -64

Здесь возникает проблема, так как получили отрицательное значение при извлечении корня из -64. Это значит, что заданных размеров треугольника ABC не существует и, следовательно, параллелограмма тоже не существует.

Однако, если мы предположим, что размеры заданы неверно и перепутаны местами, то можно продолжить решение.

Предположим, что сторона BC имеет длину 6 см, а сторона AB имеет длину 10 см.

Теперь, чтобы вычислить площадь параллелограмма, мы можем использовать формулу: площадь = длина стороны * высоту.

Подставляя значения, получаем:
площадь = 10 см * 6 см = 60 см^2

Таким образом, если размеры заданы неверно, то площадь данного параллелограмма составляет 60 квадратных сантиметров. Но стоит ознакомиться с заданием еще раз и убедиться, что размеры указаны верно.