Вычислить площадь плоской фигуры, ограниченной линиями y=x^2,y=3x.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1937,2754,1963,1900,3890,1009,2001,2010,3726 как будет на английском?...
3 - Эссе вообрвзилия 60-80 слова...
2 - Чи однакова архімедова сила діе на тіло у воді та в нафті?...
3 - На вход программе подаются три целых числа, программа сначала должна...
1 - вас мне, у меня критическая ситуация...
3 - АЙТЫЛЫМ 10-тапсырма. Суретке қара. Жаужүрек мың бала фильміндегі...
3 - Твір сильний характер а екстемальній ситуації...
2 - 1. Составьте характеристику Дины, придерживаясь пунктов плана и...
2 - ЛЕТНИЙ ВЕЧЕР Последние лучи закатаЛежат на поле сжатой ржи.Дремотой...
3 - Rinklin.png Длина радиуса OB = 14 см 8 мм. Определи длину диаметра...
3
Приравняем данные функции и решим полученное уравнение:
Теперь найдём интеграл по формуле Ньютона-Лейбница:
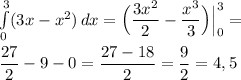
ответ: