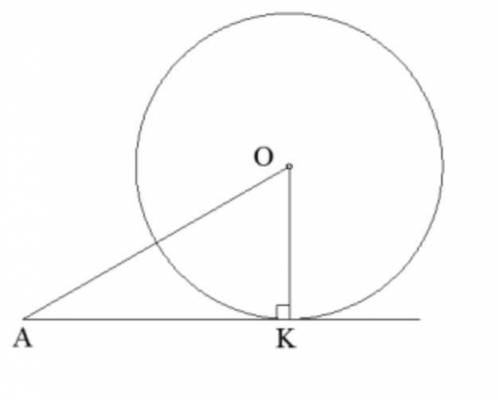
Вычисли радиус окружности, если отрезок касательной
AK=8√3дм и ∢OAK=30°.
Другие вопросы по теме Геометрия
Популярные вопросы
- Заданы вектора a =(5; - 2) и b=(2; 1) найдите координаты вектора c=a+b...
3 - Даны переменные см. Рис. Выберите ответ в котором верно указан тип каждой...
2 - Даны вектора а {5; -1; 2} и b {3; 2; - 4} найдите |а - 2b|...
1 - В войне с Дарием 1 саки придерживались тактики (более 1 правильного...
1 - А кто 32*b-59=453 398+4907:k=405...
3 - Папишите пять вопросов по повести Выстрел условие: выбор ответа НАПРИМЕР:кто...
2 - 2х-6 ≤43х-4 2 У МЕНЯ СОЧ...
1 - III. Rewrite the phrases in bold using an appropriate modal and making...
3 - 3 Write a word or phrase from the box in each gap. agree • by mistake...
3 - Автомобиль под действием силы тяги 300 Н проходит расстояние 20 м. Вычислите...
2
Дано: AK = 8√3 дм, ∠OAK = 30°.
Определение: Тангенциальная окружность - это окружность, которая касается отрезка в одной точке, которая называется точкой касания.
Нам дан отрезок AK, который является касательной к окружности. Для того чтобы найти радиус окружности, нам нужно найти расстояние от точки касания до центра окружности (точки O).
Шаг 1: Рассмотрим треугольник OAK.
- AK - сторона треугольника, известная длина.
- ∠OAK - угол, известная величина.
- Радиус окружности - искомая величина.
Шаг 2: Применим теорему синусов, которая гласит:
sin(∠OAK) / AK = sin(∠AKO) / OA
Мы знаем значение ∠OAK и AK, поэтому можем использовать эту формулу для нахождения OA.
Шаг 3: Подставим значения в формулу и решим её.
sin(30°) / 8√3 = sin(∠AKO) / OA
Поскольку sin(30°) = 1/2, и 8√3 - это 8 * √3, то получаем:
1/2 / 8√3 = sin(∠AKO) / OA
Упростим левую часть:
1 / (2 * 8√3) = sin(∠AKO) / OA
Упростим правую часть:
sin(∠AKO) может быть найдено используя дополнительный угол:
∠AKO + ∠OAK = 180°
∠AKO + 30° = 180°
∠AKO = 150°
Поскольку sin(150°) = 1/2, то получаем:
1/2 / OA = 1/2
OA = 1/2
Поскольку OA - это радиус окружности, получаем:
Радиус окружности = 1/2 дм (или 0.5 дм)
Ответ: радиус окружности равен 0.5 дм.