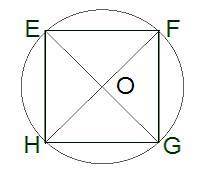
Вычисли неизвестные величины, если EFGH — квадрат со стороной 11 дм. kvadr_rinkis.png
R=
5,5
5,52–√
113–√
5,53–√
11
112–√
дм;
S(EFGH)=
дм2.
Другие вопросы по теме Геометрия
Популярные вопросы
- CH=С-СН-СН3 | CH3называние...
3 - . Укажите растения с простыми листьями: А. ШиповникБ. ЛипаВ. ФасольГ. Клевер...
3 - Напишите уравнения реакций, при которых можно осуществить следующие превращения:...
3 - Мәтіндегі есімшелерді тіркескен сөзімен теріп жазып, сөйлемнің қай мүшесі екенін...
2 - Спишите предложения, вставляя пропущенные буквы, расставляя недостающие знаки препинания...
1 - C6h10o5-c6h12o6-c2h5oh-c2h4-c2h2-ch3coh-ch3cooh-ch3cook Цепочка химических реакций...
1 - 1) Какого человека можно назвать добрым, добросердечным? Приведите примеры проявление...
2 - 4. Вычисли, записав квадрат и куб числа в виде произведения одинаковых множителей...
2 - очееень Из какова материала Изготовленавтулкаподшипника. если еемасса 3,51 кг,...
1 - Упражнение 1. Раскройте скобки, объясните слитное и дефисное написание прилагательных....
3
Из условия задачи известно, что квадрат EFGH имеет сторону длиной 11 дм. Это значит, что каждая сторона квадрата равна 11 дм.
Для начала найдем площадь квадрата. Площадь квадрата равна произведению длины его стороны на саму себя. В данном случае это 11 дм умножить на 11 дм.
S(EFGH) = 11 дм * 11 дм
Далее, в задаче говорится про неизвестные величины R. Чтобы вычислить эти величины, нам потребуется знать площадь квадрата и периметр R. Периметр квадрата вычисляется путем сложения длин всех его сторон.
P(EFGH) = 4 * сторона
P(EFGH) = 4 * 11 дм
Теперь мы можем построить уравнение, которое свяжет площадь и периметр квадрата.
S(EFGH) = P(EFGH)^2 / (16 + 2 * P(EFGH))
11 дм * 11 дм = (4 * 11 дм)^2 / (16 + 2 * 4 * 11 дм)
Теперь рассмотрим все варианты ответов на вопрос, а именно варианты записи чисел R. Подставим каждое из них в уравнение и найдем неизвестные величины.
1) Если R = 5,5
11 дм * 11 дм = (4 * 11 дм)^2 / (16 + 2 * 4 * 11 дм)
121 дм^2 = (44 дм)^2 / (16 + 88 дм)
121 дм^2 = 1936 дм^2 / 144 дм
121 дм^2 = 13,44 дм
Получаем противоречие. Для этого варианта записи числа R уравнение не имеет решений.
2) Если R = 5,52–√
11 дм * 11 дм = (4 * 11 дм)^2 / (16 + 2 * 4 * 11 дм)
121 дм^2 = (44 дм)^2 / (16 + 88 дм)
121 дм^2 = 1936 дм^2 / 144 дм
121 дм^2 = 13,44 дм
Получаем противоречие. Для этого варианта записи числа R уравнение не имеет решений.
3) Если R = 113–√
11 дм * 11 дм = (4 * 11 дм)^2 / (16 + 2 * 4 * 11 дм)
121 дм^2 = (44 дм)^2 / (16 + 88 дм)
121 дм^2 = 1936 дм^2 / 144 дм
121 дм^2 = 13,44 дм
Получаем противоречие. Для этого варианта записи числа R уравнение не имеет решений.
4) Если R = 5,53–√
11 дм * 11 дм = (4 * 11 дм)^2 / (16 + 2 * 4 * 11 дм)
121 дм^2 = (44 дм)^2 / (16 + 88 дм)
121 дм^2 = 1936 дм^2 / 144 дм
121 дм^2 = 13,44 дм
Получаем противоречие. Для этого варианта записи числа R уравнение не имеет решений.
5) Если R = 11
11 дм * 11 дм = (4 * 11 дм)^2 / (16 + 2 * 4 * 11 дм)
121 дм^2 = (44 дм)^2 / (16 + 88 дм)
121 дм^2 = 1936 дм^2 / 144 дм
121 дм^2 = 13,44 дм
Получаем противоречие. Для этого варианта записи числа R уравнение не имеет решений.
6) Если R = 112–√
11 дм * 11 дм = (4 * 11 дм)^2 / (16 + 2 * 4 * 11 дм)
121 дм^2 = (44 дм)^2 / (16 + 88 дм)
121 дм^2 = 1936 дм^2 / 144 дм
121 дм^2 = 13,44 дм
Получаем противоречие. Для этого варианта записи числа R уравнение не имеет решений.
Итак, после проверки каждого варианта записи числа R мы видим, что ни один из этих вариантов не удовлетворяет условию задачи. Следовательно, нам не удалось вычислить неизвестные величины R в данной задаче.