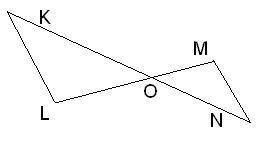
Вычисли неизвестную сторону, если дано, что ΔMNO∼ΔLKO. MO= 4 LO= 28 ON= 6;
OK=
Другие вопросы по теме Геометрия
Популярные вопросы
- Садик мой весёлый, где же твои цветы? под дождём осенним изменился как тебя...
3 - 3гади, 3 кушма составить предложение на татарском языке 3 простых и 3 сложных...
3 - Два тракториста вспахали 12,32 га земли, причём один из них впахали в 1,2...
2 - Выберите предложении в котором есть притяжательное местоимение : образование...
2 - Назовите фамилие барина из произведения мертвые души...
1 - 1) сплав состоит из олова и свинца, массы которых относятся как 2 : 3. масса...
2 - Express the same in english. 1. рост моей двоюродной сестры 1 м 75 см. если...
2 - Айжаннын ашекей буйымдар салатын кобдишасына и-дан басталатын создер тусип...
1 - Через річку проходить міст. ширина річки 80 м. чверть моста розташована...
2 - Сделать проект о важном событии 4 класс...
2
коеф,подібності = 28/4= 7
ОК= 7*6= 42
1) Соотношение длин сторон: в подобных треугольниках отношение длин любых двух сторон равно. Из условия дано, что ΔMNO∼ΔLKO, поэтому мы можем установить следующее соотношение:
MO/LO = NO/KO
2) Соотношение длин высот треугольников: в подобных треугольниках отношение длин высот равно отношению длин сторон. Высота треугольника - это перпендикуляр, опущенный из вершины треугольника к противоположной стороне. В данной задаче нам не даны длины высот, но мы можем использовать соотношение длин высот для решения задачи. Пусть H1 и H2 - высоты треугольников ΔMNO и ΔLKO соответственно. Тогда мы можем записать следующее соотношение:
H1/H2 = MO/KO
Теперь мы можем приступить к решению задачи:
1) Соотношение длин сторон:
MO/ LO = NO/KO
4/28 = 6/KO
Мы хотим найти значение ОК (KO), поэтому мы выразим ОК (KO) через уже известные значения и неизвестное значение:
4/28 = 6/KO
KO = 6 * 28 / 4
KO = 3 * 28
KO = 84
Таким образом, длина ОК (KO) равна 84.