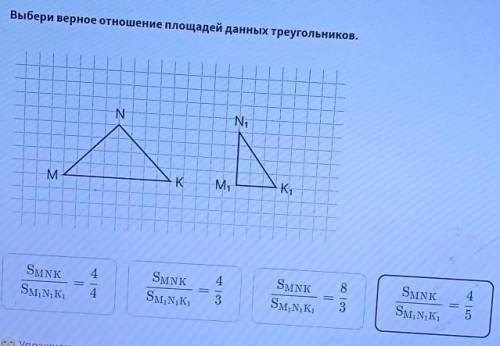
Выбери верное отношение площадей данных треугольников

Для решения этого вопроса, нам нужно сравнить площади треугольников.

Давайте обозначим треугольник на левой стороне как Треугольник А и треугольник на правой стороне как Треугольник В.

Чтобы найти площадь треугольника, мы можем использовать формулу площади треугольника, которая составляется путем умножения половины основания на высоту треугольника.

Формула для площади треугольника: Площадь = 0,5 * Основание * Высота

Для Треугольника А, длина его основания составляет 4 см, а высота составляет 6 см.
Давайте подставим значения в формулу площади треугольника:
Площадь Треугольника А = 0,5 * 4 см * 6 см = 12 см²

Для Треугольника В, длина его основания составляет 6 см, а высота составляет 4 см.
Давайте подставим значения в формулу площади треугольника:
Площадь Треугольника В = 0,5 * 6 см * 4 см = 12 см²

Теперь у нас есть значения площадей обоих треугольников. Сравнивая их, мы видим, что оба треугольника имеют одинаковую площадь, которая составляет 12 см².

Поэтому, верное отношение между площадями данных треугольников - они равны.

Основание и высота треугольника могут быть диагоналями, но для нашего примера, мы использовали прямоугольные треугольники с одной стороной на горизонтальной оси и одной стороной на вертикальной оси. В реальных ситуациях, основание и высота треугольника могут быть разными и по-разному ориентированы.