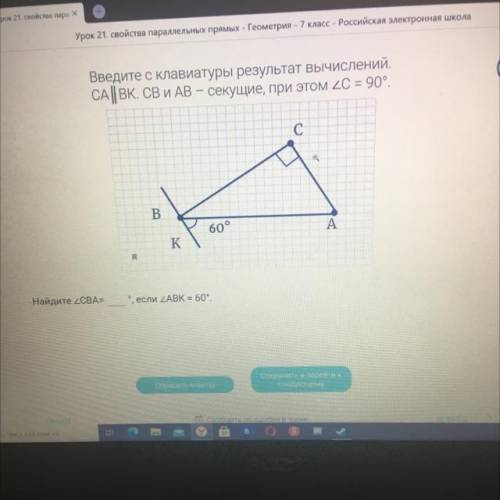
Введите с клавиатуры результат вычислений.
СА || ВК. СВ и АВ – секущие, при этом C= 90°.
Найдите CBA=
°, если ABK = 60°

Другие вопросы по теме Геометрия
Популярные вопросы
- Решить 2 класс заполни пропуски и выполни действие с числового...
1 - Отзыв о сказке ивины (из повести детство ,в сокращении) заранее...
1 - А)составь описание матрешки на основе двух текстов к.г паустовского.б)составь...
1 - Найдите значение выражения: скобка корень из двух плюс один скобка...
1 - Почему 15 в называют золотым веком крестьян в европе...
3 - Вариант 1. ткани, клетки которых располагаются тесными в один...
2 - Связь биологических дисциплин с другими науками...
2 - Примеры того как выполнение одной работы препятствует выполнению...
3 - Ракета,запущенная с земли на луну,пролетает расстояние 410 000...
1 - Решите : а)-0,4y(-0,8)=0,96 б)-6x3y(-5)= в)-0,2x(-0.7)=0,84 г)4,2m(-1,,5n)=...
2
1. Обозначим неизвестный угол CBA как х.
2. Из условия задачи, мы знаем, что угол ABK равен 60 градусов.
3. Заметим, что угол BKC и угол BAC являются взаимно дополнительными углами. Так как СА || ВК, то угол BKC равен 180 - 90 = 90 градусов.
4. Используя свойство углов между параллельными прямыми, мы можем сказать, что угол BAC также равен 90 градусов.
5. Так как угол BAC равен 90 градусов, то треугольник ABC является прямоугольным треугольником, и мы можем использовать теорему Пифагора для нахождения значения стороны BC.
a. Длина стороны AC равняется AB + BC = 8 + BC.
b. Длина стороны BC равняется ABK по теореме косинусов: BC = ABK*cos(ABK) = 8*cos(60) = 8*1/2 = 4.
c. Таким образом, мы имеем уравнение 8 + BC = 8 + 4 = 12.
d. Следовательно, длина стороны AC равна 12.
6. Мы можем использовать косинусы для нахождения значения угла CBA.
a. Мы знаем, что cos(CBA) = BC/AC = 4/12 = 1/3.
b. Обратившись к таблице значений тригонометрических функций, мы находим, что угол CBA должен быть около 70.53 градусов.
7. Следовательно, угол CBA ≈ 70.53 градусов.