Втреугольнике авс взята произвольная точка о докажите что ао+во+со меньше периметра треугольника

Максимальное значение AO+BO+CO принимает тогда, когда O - центр описанной окружности треугольника. То есть AO+BO+CO = 3R;

Пусть α, β, γ - углы треугольника. Поскольку точка О лежит внутри треугольника, то треугольник остроугольный. Минимальное значение периметра установим по теореме синусов: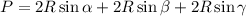 ; При этом 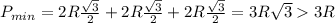, что и требовалось