1. Геометрия
  2. Втреугольнике авс угол

Втреугольнике авс угол вас= 45, угол вса= 60. длина стороны вс= корень из 3. найти площадь треугольника вос, где о- центр описанной около треугольника авс окружности

Апуля11 Апуля11    3   22.05.2019 08:20    1

Ответы
Папич3 Папич3  17.06.2020 12:15

Воспользуемся расширенной теоремой синусов, чтобы узнать радиус описанной окружности

 

\frac{BC}{\sin 45^\circ}=2R

 

\frac{\sqrt{3}}{\frac{\sqrt{2}}{2}}=2R

 

\frac{2\sqrt{3}}{\sqrt{2}}=2R

 

Сократим обе части на 2 и получим длину радиуса описанной окружности

 

R=\frac{\sqrt{3}}{\sqrt{2}}

 

R=\sqrt{\frac{3}{2}}

 

Длины сторон треугольника ВОС равны

 

BO=R=\sqrt{\frac{3}{2}},\quad OC=R=\sqrt{\frac{3}{2}},\quad BC=\sqrt{3}

 

По формуле Герона вычислим площадь треугольника ВОС

 

Сначала вычислим полупериметр

 

p=\frac{\sqrt{3}+2*\sqrt{\frac{3}{2}}}{2}

 

p=\frac{\sqrt{3}+\sqrt{6}}{2}

 

S_{\Delta BOC}=\sqrt{\frac{\sqrt{6}+\sqrt{3}}{2}*\left(\frac{\sqrt{6}+\sqrt{3}}{2}-\sqrt{3}\right)*\left(\frac{\sqrt{6}+\sqrt{3}}{2}-\sqrt{\frac{3}{2}}\right)^2}

 

 

S_{\Delta BOC}=\sqrt{\frac{\sqrt{6}+\sqrt{3}}{2}*\left(\frac{\sqrt{6}+\sqrt{3}}{2}-\sqrt{3}\right)}*\left(\frac{\sqrt{6}+\sqrt{3}}{2}-\sqrt{\frac{3}{2}}\right)

 

S_{\Delta BOC}=\sqrt{\frac{\sqrt{6}+\sqrt{3}}{2}*\left(\frac{\sqrt{6}-\sqrt{3}}{2}\right)}*\left(\frac{\sqrt{6}+\sqrt{3}}{2}-\sqrt{\frac{3}{2}}\right)

 

S_{\Delta BOC}=\sqrt{\frac{6-3}{4}\right)}*\left(\frac{\sqrt{6}+\sqrt{3}}{2}-\sqrt{\frac{3}{2}}\right)

 

S_{\Delta BOC}=\sqrt{\frac{3}{4}}*\left(\frac{\sqrt{6}+\sqrt{3}}{2}-\sqrt{\frac{3}{2}}\right)

 

S_{\Delta BOC}=\sqrt{\frac{3}{4}}*\left(\sqrt{\frac{3}{2}}+\frac{\sqrt{3}}{2}-\sqrt{\frac{3}{2}}\right)

 

S_{\Delta BOC}=\sqrt{\frac{3}{4}}*\frac{\sqrt{3}}{2}

 

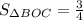S_{\Delta BOC}=\frac{3}{4}

 

ответ:S_{\Delta BOC}=\frac{3}{4} - квадратных единиц.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
sasharudich sasharudich  18.09.2019 04:10
Верно ли утверждение: если две прямые в пространстве перпендикулярны к третьей прямой,то эти прямые параллельны? верно ли это утверждение при условии,что все три прямые...
Dania2432 Dania2432  04.05.2021 18:29
Мальчик ловил рыбу где тут главное и второстепенное ​...
altunbaevmax altunbaevmax  04.05.2021 18:29
В треугольнике АВС угол С равен 90°, tg В = 7:6, ВС =18, найдите АС...
anghelina1 anghelina1  04.05.2021 18:30
Радиус Земли будем считать равным 6 тыс.км. Определите площадь земной поверхности....
lalka137 lalka137  04.05.2021 18:30
570. У рівнобедреному трикутнику з вершини одного кута при основі проведено висоту трикутника, аз вершинибісектрису трикутника. Одиніз кутів, утворених при перетині...
2маша 2маша  04.05.2021 18:33
У прямокутному трикутнику висота, проведена до гіпотенузи, дорівнює 24 см і ділить її на відрізки у відношенні 9 1: 6 . Знайди довжину гіпотенузи....
cvacvadav cvacvadav  22.05.2020 12:26
Укажіть у якому випадку точки В,С і D не належать одній прямій А)ВС=18. ВD= 10 CD=8 Б) BC=20 BD=12 CD=10В)ВС=19 ВD=6 СD=25Г) ВС= 17 ВD=24 CD=7​...
svetasvetashi svetasvetashi  22.05.2020 12:24
до У рівнобедреному трикутнику ABC з основою AC сума кутів A i C дорівнює 166(градусів). Знайдіть усі невідомі внутрішні і зовнішні кути трикутника ABC. І ще 2 запитання....
BarcelonaReal BarcelonaReal  22.05.2020 12:24
Дана окружность с центром O и её диаметры AB и CD.Определи периметр треугольника AOD, если CB = 12 см, AB = 65 см.1. Назови свойство радиусов окружности: все радиусы...
pro00losk pro00losk  22.05.2020 12:24
решите надо Точка М лежит на отрезке KF. Сравните длины отрезков: А) KM MF Б) KM = MF В) KF KM Г) KM KF 3. Найдите периметр треугольника DCE , если DE равно 11 см, CD...

Популярные вопросы