Втреугольнике авс ав=15 см, ас=20 см, вс=32 см. на стороне ав отложен отрезок аd=9 cм а на стороне ас отложен отрезок ае=12 см.

Question

Геометрия: Втреугольнике авс ав=15 см, ас=20 см, вс=32 см. на стороне ав отложен отрезок аd=9 cм а на стороне ас отложен отрезок ае=12 см. найти de и отношение площадей треугольника авс и аd. можно с рисунком

Annarasumanara2002 · Answer

Поскольку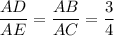 и общий, то треугольник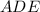и и 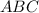подобны по двум пропорциональным сторонам и углу между ними. Из подобия треугольников следует соотношение:                       см.Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. В нашем случае коэффициент подобия , поэтому отношение площадей треугольника ABC и ADE:                                            ...

Популярные вопросы