Втреугольнике abc отмечены середины m и n сторон bc и ac соответственно. площадь треугольника cnm равна 89. найдите площадь четырехугольника abmn
Ответы
MN - средняя линия треугольника ABC, по теореме о средней линии NM=AB/2 => 2NM=AB Проведем высоту из вершины С. SCNM=1/2*CE*NM=89 (по условию).CE*NM=178 Рассмотрим треугольник ACD, NE||AD и идет из середины стороны AC, следовательно NE - средняя линия для треугольника ACD, значит CE=ED. ABMN - трапеция (по определению), тогда SABMN=(NM+AB)/2*ED. Подставляем ранее выявленные равенства, получаем: SABMN=(NM+2NM)/2*CE=3NM/2*CE=1,5NM*CE=1,5*178=267
ПОКАЗАТЬ ОТВЕТЫ
....................
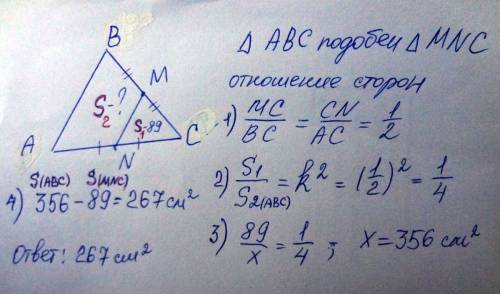
ПОКАЗАТЬ ОТВЕТЫ
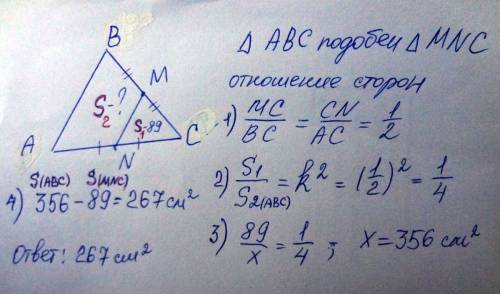
Другие вопросы по теме Геометрия
Популярные вопросы
- Во сколько раз площадь треугольника abc больше площади треугольника...
3 - Радиус окружности описанной около правильного треугольника равен...
3 - Масса 3 кусков мрамора - 280 кг. 1 кусок на 32 кг тяжелее 2-го, а...
2 - Кто в афинах считался гражданином? какими правами обладал афинский...
3 - Составте 5 предложений к следующиму тексту: the aim of all schoolchildren...
3 - Найди правильную a. (3b-c)(3b+c)=9b^2-c^2 b. (x+4)(4-x)=16-x^2 c....
2 - Средняя скорость лыжника 15 км/ч,а другого 200м/мин.какой лыжник...
3 - За контрольную работу 12 человек получили отметку 5, 20 человек -...
1 - Почему могут возникнуть конфликты между местным населением и пришлым?...
2 - Найти ошибки, в каких случаях есть два варианта( название): старинное...
2