Втрапеции abcd с основаниями ad=12 и вс=8, боковыми сторонами ав=7 и cd=11 биссектрисы углов а и в пересекаются в точке р, а биссектрисы углов с и

Question

Геометрия: Втрапеции abcd с основаниями ad=12 и вс=8, боковыми сторонами ав=7 и cd=11 биссектрисы углов а и в пересекаются в точке р, а биссектрисы углов с и d – в точке q. найдите длину отрезка pq.

seletkovaolya · Answer

По свойству биссектрисы, она равноудалена от сторон которые её образуют.

Значит биссектриса из угла A равноудалена от сторон AD и AB, а биссектриса из угла B равноудалена от сторон AB и BC => точка пересечения биссектрис(P) равноудалена от сторон AB,AD и BC значит она лежит на средней линии трапеции (MN).

Аналогично точка Q лежит на средней линии трапеции.

-----------------

Рассмотрим треугольник ABP, как известно сумма односторонних углов трапеции=180°, значит сумма их половинок=90°.

Значит ∠APB=180-90=90°.

Аналогично ∠DQC=90°.

Отрезки PM и QN - это медианы опущенные из прямых углов, они равны половине гипотенузы.

---------------------

Искомый отрезок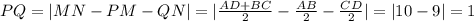 $PQ=|MN-PM-QN|=|\frac{AD+BC}{2}-\frac{AB}{2}-\frac{CD}{2}|=|10-9|=1$