,всё прикреплено
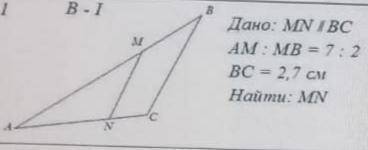
MN||BC,AM:MB=7:2,BC-2,7 Найти MN

Для решения данной задачи, мы можем воспользоваться свойством параллельных прямых. Из условия задачи видно, что прямые MN и BC параллельны. Поэтому, угол MBC и угол MNB являются соответственными углами, образованными при пересечении этих прямых с прямой AB. Также, по условию, известно, что отношение AM к MB равно 7:2. Мы можем воспользоваться соотношением, которое выражает соответствующие части параллельных сторон треугольников. Оно гласит, что отношение длин отрезков, соответствующих параллельным сторонам треугольников, равно отношению длин соответствующих сторон треугольников. То есть, можем записать следующее соотношение: AM / MB = AC / CB Мы знаем, что AM / MB = 7 / 2. Пусть значением отношения AC / CB будет х. Тогда мы можем записать уравнение: 7 / 2 = х Перекрестным умножением, получаем: 7 * CB = 2 * AC CB = 2AC / 7 Теперь, поскольку мы знаем, что BC равно 2,7, мы можем записать следующее уравнение: CB = 2,7 Используя это уравнение, мы можем найти значение AC: 2AC / 7 = 2,7 Перекрестным умножением, получаем: 2AC = 2,7 * 7 2AC = 18,9 AC = 18,9 / 2 AC = 9,45 Теперь у нас есть значение AC. Из треугольника ABC, приходим к выводу, что MC = AC - AM. Заменяя значения, имеем: MC = 9,45 - 7 MC = 2,45 Таким образом, мы нашли значение отрезка MC. Заметим, что из треугольника MNC, MN равно MC - BC. Заменяя значения, имеем: MN = 2,45 - 2,7 MN = -0,25 Таким образом, MN равно -0,25. Ответ: MN = -0,25.