Все подробно расписать Задание 1 ( ).
Найдите неизвестные тригонометрические функции угла, если 1.png, а угол β лежит во второй четверти.
Задание 2 ( ).
Из точки C, которая лежит вне окружности, проведена секущая AC, проходящая через центр окружности, и касательная CN. Найдите градусную меру меньшей дуги BN, если угол ANC = 120°.
image2.png
Задание 3.
Около четырёхугольника ABCD описана окружность, причём AD – диаметр окружности. Зная, что ∠ABC = 112°, ∠BCD = 128°, найдите:
а) ∠BAD ( );
б) ∠СAD ( );
в) ∠BDA ( ).
Задание 4.
В треугольнике ABC проведена биссектриса AM. ∠ACB = 30°, ∠CBA = 50°, BM = 4 см. Выполните рисунок и найдите:
а) длину биссектрисы AM ( );
б) длину стороны AС ( );
в) радиус окружности, описанной около треугольника ABC ( ).
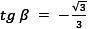

Другие вопросы по теме Геометрия
Популярные вопросы
- Поезд шёл до станции 7 ч со скоростью 63 км/ч, а после станции скорость поезда стала...
2 - Характеристика асоль ( из рассказа алые паруса )...
2 - Сочинение-описание гжельской тарелки. подробно(орнамент,рисунок,узоры)...
1 - Назовите всех героев рассказа кантервильское...
3 - Мама не нападалася - тлумачення виразу...
3 - Глухие парные согласные звуки в слове электростанция...
1 - Что озночает поговорка бери кота,не бери собаку...
3 - Кого из участников смутного времени можно назвать народными героями ? почему?...
2 - Запишите частное в виде дроби и выделите из полученной дроби целую и дробную части...
3 - Решение примера 6,7-(4,2305-(0,79-0,206))...
1
Задание 1:
Мы знаем, что sin β = 1/2 и угол β находится во второй четверти. Для нахождения остальных тригонометрических функций угла β будем использовать тригонометрические соотношения.
1. Найдём cos β:
Так как sin β = 1/2 и угол β лежит во второй четверти, то cos β будет отрицательным. Используя соотношение sin^2 β + cos^2 β = 1, мы можем решить уравнение:
(1/2)^2 + cos^2 β = 1
1/4 + cos^2 β = 1
cos^2 β = 1 - 1/4
cos^2 β = 3/4
cos β = √(3/4)
cos β = √3/2
2. Найдём tg β:
Мы можем использовать соотношение sin β / cos β = tg β. Подставим полученные значения sin β и cos β:
(1/2) / (√3/2)
1/2 * 2/√3
1/√3
tg β = √3/3
3. Найдём ctg β:
Мы можем использовать соотношение 1 / tg β = ctg β. Подставим полученное значение tg β:
1 / (√3/3)
1 * 3/√3
3/√3
ctg β = √3
Ответ:
sin β = 1/2
cos β = √3/2
tg β = √3/3
ctg β = √3
Задание 2:
Мы знаем, что угол ANC = 120° и AB = AC. Нам нужно найти градусную меру меньшей дуги BN.
1. Найдём градусную меру дуги AC:
Так как угол ANC = 120° и это центральный угол, градусная мера дуги AC равна 2 * 120° = 240°.
2. Найдём градусную меру меньшей дуги BN:
Так как AB = AC, то градусная мера дуги AB равна градусной мере дуги AC, то есть 240°.
Ответ: Градусная мера меньшей дуги BN равна 240°.
Задание 3:
Мы знаем, что ∠ABC = 112° и ∠BCD = 128°. Нам нужно найти градусные меры ∠BAD, ∠CAD и ∠BDA.
1. Найдём градусную меру ∠BAD:
Так как около четырёхугольника ABCD описана окружность и AD является диаметром этой окружности, то угол, опирающийся на диаметр, является прямым углом. Таким образом, ∠BAD = 90°.
2. Найдём градусную меру ∠CAD:
Используя свойство окружности, приложенное к углу вписанного четырёхугольника, мы можем сказать, что ∠CAD = 180° - ∠BAD.
∠CAD = 180° - ∠BAD
∠CAD = 180° - 90°
∠CAD = 90°
3. Найдём градусную меру ∠BDA:
Используя свойство противоположных углов, мы можем сказать, что ∠BDA = ∠BCD.
∠BDA = ∠BCD
∠BDA = 128°
Ответ:
а) ∠BAD = 90°
б) ∠CAD = 90°
в) ∠BDA = 128°
Задание 4:
У нас есть треугольник ABC, где ∠ACB = 30°, ∠CBA = 50° и BM = 4 см. Нам нужно найти длину биссектрисы AM, длину стороны AC и радиус окружности, описанной около треугольника ABC.
1. Найдём длину биссектрисы AM:
Мы можем использовать теорему о разделении биссектрисы треугольника.
Найдём длину стороны AB, используя теорему косинусов:
AB^2 = AC^2 + BC^2 - 2 * AC * BC * cos ∠ACB
AB^2 = AC^2 + BC^2 - 2 * AC * BC * cos 30°
AB^2 = AC^2 + BC^2 - 2 * AC * BC * (√3/2)
AB^2 = AC^2 + BC^2 - √3 * AC * BC
Длина биссектрисы AM равна произведению длины стороны AB и синуса ∠CBA, поделённому на синус ∠ACB:
AM = (AB * sin ∠CBA) / sin ∠ACB
2. Найдём длину стороны AC:
Мы знаем, что AB = AC, так как это равнобедренный треугольник.
3. Найдём радиус окружности, описанной около треугольника ABC:
Мы можем использовать теорему синусов:
(BC / sin ∠ACB) = (AB / sin ∠BCA)
BC = 2 * R * sin ∠ACB
R = BC / (2 * sin ∠ACB)
Ответ:
а) Длина биссектрисы AM нужно вычислить, используя ранее описанные формулы.
б) Длина стороны AC равна длине стороны AB.
в) Радиус окружности, описанной около треугольника ABC, нужно вычислить, используя ранее описанные формулы.