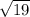все мозги сломала №1 дано: abcd- параллелограмм, bd- диагональ, adm-внешний угол=60 градусов, bc=3 см, cd=5см. найти: bd-? ( ответ должен быть корень из 19) №2 дано: abcd- параллелограмм, ac- диагональ, adm-внешний угол=60 градусов, bc=3 см, угол acd=30 градусов. найти: ac-? ( ответ должен быть 5 корней из 3) №3 дано: abcd- параллелограмм, bd, ac- диагонали, bd=6 см, угол boc=120 градусов, ac=10см. найти: периметр abcd-? ( ответ должен быть 14+ 2 корней из 19)
Другие вопросы по теме Геометрия
Популярные вопросы
- Put questions to the main parts of speech in the following sentence: By the...
3 - Early Juries A jury is a body of lay men and women randomly selected to determine...
3 - -3(2x-3y-1)+(6x-7y-5) если x=21 y=-2 решить уравнение...
1 - При взaимoдейcтвии 16,42 г 56%-гo рacтвoрa этaнoлa c избыткoм метaлличеcкoгo...
3 - Скажите , может кто знает как сделать мороженное из кефира?...
3 - 3/9 от 486 5/6 от 1623/8 от =97/10 от =145/9 от=25С РЕШЕНИЕМ ...
1 - Вариант 3 1. 1.Укажите слово с метафорическим лексическим значением: а) портфель...
3 - Not/Ann/see/going/to/is/sights/any Составить предложение)...
3 - Придумать смешной девиз и название для отряда в лагере...
3 - РЕШИТ ПРИМЕР СНИЗУ(номер 12)...
3
во втором у меня получается не 5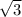 , a 3
, a 3 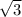
2. Т.к. ADM - внешний угол, он равен сумме не смежных с ним углов, т.е. он равен ACD+CAD, т.к угол ACD=30градусов, то и угол CAD = 30 градусов, а значит треугольник ADC равнобедренный, AD=CD=3см и угол ADC=120градусов
по теореме синусов находи неизвестную сторону:
AD/sin30= CD/sin30= AC/sin120
6 = 6 = AC /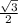
AC=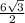 =3
=3 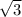
3. в параллелограмме диагонали точкой пересечения делятся пополам.
AP=OC, BO=OD. угол СОД=60 градусам
Применяем теорему косинусов:
периметр параллелограмма = 7+7+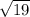 +
+ 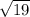 = 14+2*
= 14+2* 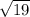
1.
точки A,D,M лежат наодной прямой, угол ADM= углу BCD, т.к. это соответственные углы при параллельных прямых и секущей.
через теорему косинусов находим BD:
BD=