Вравнобедренном треугольнике abc о - точка персечения медиан. найдите расстояние от точки о до вершины a данного треугольника, если ab=bc=10 см, ac=16 см

АО-радіус описаного кола
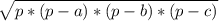
R=abc/4S де а.b.c сторони трикутника, S-його площа
S можна знайти за формою герона

p-пів периметр p=(a+b+c)/2

Так-с, у нас есть равнобедренный треугольник ABC. Достраиваем в нем медианы: BQ к AC и AE к BC. Этого хватит. Рассмотрим треугольник ABQ: BQ будет перпендикуляром, так как в равнобедренных треугольниках( в данном случае ABC) медиана, проведенная к основанию является так же и высотой. Следовательно, угол AQB=90 градусов. AB=10см, AQ=1/2*AC=8см, так как BQ - медиана. Теперь из прямоугольного треугольника ABQ найдем катет BQ по теореме Пифагора: BQ=корень из (AB^2-AQ^2)=корень из (10*10-8*8)=корень из (100-64)=корень из 36=6см. В равнобедренном треугольниках пересекаются в одной точке и делят друг друга на отрезки в отношении 2/1 считая от вершины. Следовательно, BO/OQ=2/1. BO=4см, OQ=2см. И теперь осталось найти AO из треугольника AOQ, где угол AQB равен 90 градусов, по теореме Пифагора: AO=корень из (OQ^2+AQ^2)= корень из (4+64)=корень из 68=4*корень из 17