1. Геометрия
  2. Впрямоугольном треугольнике

Впрямоугольном треугольнике авс с катетами вс=8, ас=10 через центр о описанной около треугольника окружности проведена прямая, перпендикулярная его гипотенузе и пересекающая больший катет в точке к. найдите длину отрезка ак.

nbis2000 nbis2000    1   05.10.2019 19:00    9

Ответы
ьпоаь1 ьпоаь1  09.10.2020 22:15

По теореме Пифагора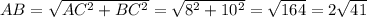 AB=\sqrt{AC^2+BC^2}=\sqrt{8^2+10^2}=\sqrt{164}=2\sqrt{41}

Т.к. центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы, то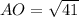 AO=\sqrt{41}

ΔABC ≈ ΔAOK (по трем углам) ⇒

\frac{AO}{AC}=\frac{AK}{AB}\\AK=\frac{AO*AB}{AC}=\frac{\sqrt{41}*2*\sqrt{41}}{10}=\frac{82}{10}=8.2


Впрямоугольном треугольнике авс с катетами вс=8, ас=10 через центр о описанной около треугольника ок
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
мууур1 мууур1  08.07.2019 05:00
Является ли параллелограмм выпуклым четырехугольником?...
markdanilov2002 markdanilov2002  08.02.2022 00:30
Квадрат со стороной 11 корень 2 вписан в окружность. Найди длину окружности....
tatarchenko04 tatarchenko04  08.02.2022 00:25
Можно подробное решение, с доказательствами очень нужно оформление к 10...
Пчка Пчка  08.02.2022 00:23
Треугольник ABC и CDE подобны. Найти углы треугольника CDE, если A=38°, угол C=50°...
ervinbek2005 ervinbek2005  08.02.2022 00:21
ТЕСТ 1. Заполните пропуски(многоточия), чтобы получилось верное высказывание. 1.Если стороны прямоугольника являются хордами окружности, то окружность называется……………...
френки9 френки9  08.02.2022 00:18
9. Дано: ABCD – прямоугольник, BF  AB, AF  AD, BD = 7, DF = 25. Найдите SBDF....
Лиро1 Лиро1  12.09.2019 12:20
X^2+y^2+z^2+2z+4y+6z+a=0 определите при каких значениях а задает сферу...
SobolVitalik SobolVitalik  12.09.2019 12:20
Дано: угол acb=acd. ac биссектриса угла bad. доказать что abc = adc...
zuzin77 zuzin77  16.11.2019 12:31
T3в равнобедренном треугольнике авсс основанием ас внешний угол привершине с равен 144°. найдитевеличину угла abc. ответ дайтев градусах.ответ: ​...
КириллПос КириллПос  16.11.2019 12:28
Точка с - середина отрезка ab, пересекающего плоскость альфа в точке м.через точки а, с и b проведены параллельные прямые, пересекающие плоскость альфа соответственно...

Популярные вопросы