Впрямоугольном треугольнике ABC угол C = 90°, катеты a и b соответственно равны корень11 cm и 5 cm. Найдите гипотенузу c, острые углы a и

Question

Геометрия: Впрямоугольном треугольнике ABC угол C = 90°, катеты a и b соответственно равны корень11 cm и 5 cm. Найдите гипотенузу c, острые углы a и B этого треугольника.

alinamalinachka · Answer

Для начала найдем гипотенузу этого треугольника. По теореме Пифагора, квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов его катетов.

$c^2 = a^2 + b^2\\c = \sqrt{a^2+b^2} = \sqrt{(\sqrt{11})^2+5^2} = \sqrt{11+25} = \sqrt{36} = 6$ см.

Теперь найдем острые углы этого треугольника. Сделаем это через их синусы. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. Пусть угол B лежит напротив катета b. Тогда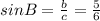 $sinB = \frac{b}{c} = \frac{5}{6}$ .

Таким образом, $B = arcsin\frac{5}{6}$ ≈ 56,44°.

Зная это, мы можем найти оставшийся угол А.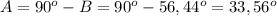 A = 90^o - B = 90^o - 56,44^o = 33,56^o .

В треугольнике напротив большей стороны всегда лежит больший угол. Значит, наше утверждение правильно. Катет b больше катета a. Поэтому угол B - тот, который лежит напротив катета b, угол A - тот, что лежит напротив катета a.

Впрямоугольном треугольнике ABC угол C = 90°, катеты a и b соответственно равны корень11 cm и 5 cm. Найдите гипотенузу c, острые углы a и B этого треугольника.

Популярные вопросы