Вправильной треугольной пирамиде боковое ребро равно 7. сторона основания 4. найти высоту пирамиды

Question

Геометрия: Вправильной треугольной пирамиде боковое ребро равно 7. сторона основания 4. найти высоту пирамиды

Klobutska · Answer

Обозначим пирамиду МАВС, МО - высота пирамиды. МО перпендикулярна основанию пирамиды.

О - центр описанной окружности около основания АВС данной пирамиды.

Все углы правильного треугольника равны 60°. По т.синусов радиус АО описанной окружности равен

R=AO:2sin60°

Если условие задано верно и сторона основания равна 4, то:

$R=4:2* \frac{ \sqrt{3}}{2} = \frac{4}{ \sqrt{3}}$

Тогда по т.Пифагора из прямоугольного ∆ АМО высота

МО=√(AM²-AO²)=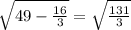 $\sqrt{49- \frac{16}{3} } = \sqrt{ \frac{131}{3}} }$

Но эта задача обычно задается со стороной основания, равной 4,5

Тогда условие задачи: В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания 4,5. Найдите высоту.

Для этого значения

R=4: 2√3/2=4,5:√3=1,5•√3

По т.Пифагора высота пирамиды

МО=√(МА²-АО²)=√(49-2,25•3)=6,5 (ед. длины)