1. Геометрия
  2. Вправильной четырехугольной

Вправильной четырехугольной пирамиде сторона основания равна 8см, а боковое ребро наклонено к плоскости основания под углом 45 градусов. найти площадь боковой поверхности пирамиды.

224678 224678    1   21.05.2019 14:30    1

Ответы
fomicheva3ket fomicheva3ket  16.06.2020 00:23

Поскольку четырехугольная пирамида ПРАВИЛЬНАЯ, то в основании лежит квадрат. Диагональ квадрата ABCD равен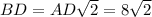 BD=AD\sqrt{2} =8\sqrt{2} см. Диагонали квадрата пересекаются в точке О и точка О делит диагонали пополам, то есть 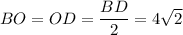BO=OD=\dfrac{BD}{2} =4\sqrt{2} см.

Из прямоугольного треугольника SOD: из определения косинуса найдем боковое ребро пирамиды:

\cos \angle \mathrm{SDO}=\dfrac{\mathrm{OD}}{\mathrm{SD}} ~~\Rightarrow~~ \mathrm{SD}=\dfrac{\mathrm{OD}}{\cos45а} =\dfrac{4\sqrt{2}}{1/\sqrt{2}} =8 см.

Высота SK равнобедренного треугольника SCD делит основание CD пополам, то есть: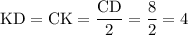 \mathrm{KD=CK=\dfrac{CD}{2}=\dfrac{8}{2}=4} см

Тогда из прямоугольного треугольника SKC:

\mathrm{SK=\sqrt{SC^2-CK^2}=\sqrt{8^2-4^2}=4\sqrt{3}} см. Тогда площадь грани SCD равна \displaystyle \mathrm{S_{SCD}=\frac{CD\cdot SK}{2}=\frac{8\cdot 4\sqrt{3}}{2}=16\sqrt{3}} см²

Площадь боковой поверхности - это сумма всех площади граней. То есть, зная что у правильной пирамиды все грани равны, то площадь бок. пов.

\mathrm{S_{bok}=4\cdot S_{SCD}=4\cdot 16\sqrt{3}=64\sqrt{3}} см²

ответ: 64√3 см².


Вправильной четырехугольной пирамиде сторона основания равна 8см, а боковое ребро наклонено к плоско
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Вайнесс Вайнесс  10.04.2020 09:55
(1+tga)²+(1-tga)² с вираз и знайти його значення якщо cosa=0.6...
avaitekhovich avaitekhovich  10.04.2020 09:55
1. на данном луче от его начала отложить отрезок, равный данному.2. Построение угла, равного данному.3. Построение биссектрисы угла.4. Построение перпендикулярных прямых.5....
Maksi112 Maksi112  10.04.2020 09:55
Найдите острые углы прямоугольного треугольника, если один из них в 5 раз больше другого....
Vitas40 Vitas40  10.04.2020 09:55
Дано: окружность, CD=d, АВ-хорда, CDN AB=E угол AED=30°, DE=12 см,АС=4см Найти: ОКРешение: 1) CD =12+4=16см,= СО-ОD=r=8см, EO= CD OD + EC) -16-(4+8) -4 см 2)рассмотрим...
valeria204567 valeria204567  03.10.2019 19:01
Втреугольнике abc угол c равен 90° ch высота угол а равен 45° ab =1.найди bh...
ввіна ввіна  03.10.2019 19:01
Ознаки рівності рівнобедреного трикутника...
IIIayni IIIayni  03.10.2019 19:10
34 .концы бокового ребра правильной треугольной призмы удалены от противолежащей этому ребру стороны основания на 2 м и 4 м. найти площадь боковой поверхности призмы....
YTMrBreadYT YTMrBreadYT  16.04.2021 18:58
Хорда АС стягивает дугу окружности в 60°. В точке А проведена касательная к этой окружности. Найдите величину угла между касательной и хорды ​...
Марина19r Марина19r  16.04.2021 18:57
Через кінці діаметра АВ кола проведено паралельні хорди ВС і АD. Доведіть, що АD = BC​...
ПОМОГИТЕ13217 ПОМОГИТЕ13217  16.04.2021 18:56
Прямі МА і МВ дотикаються до кола з центром О в точках А і В. Знайдіть АВ, якщо ОМА =30, АМ = 6 см...

Популярные вопросы