1. Геометрия
  2. Впараллелограмме abcd

Впараллелограмме abcd точка e - середина стороны ab. известно, что ec = ed. докажите , что данный параллелограмм - прямоугольник

AliskaLao16 AliskaLao16    3   04.10.2019 16:57    0

Ответы
iruha07082001 iruha07082001  09.10.2020 20:03

Что и требовалось доказать!

Объяснение:

Так как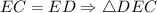 EC = ED \Rightarrow \triangle DEC - равнобедренный ⇒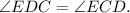 \angle EDC = \angle ECD.

В параллелограмме противоположные стороны параллельны.

\Rightarrow AB || CD \Rightarrow AE || CD \: \: u \:\: EB || CD.

При пересечении двух параллельных секущей, накрест лежащие углы равны.

\Rightarrow \angle EDC = \angle AED, \:\: \angle ECD = \angle BEC.

Но так как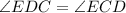 \angle EDC = \angle ECD, по свойству ⇒

\angle ECD = \angle EDC = \angle AED = \angle BEC.

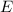Так как E - середина AB ⇒ AE = EB.

CE = ED, по условию.

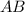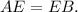
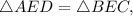⇒ \triangle AED = \triangle BEC, по 1 признаку равенства треугольников.

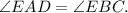
⇒ \angle EAD = \angle EBC.

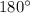В параллелограмме сумма односторонних углов равна 180^{\circ}.

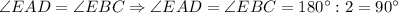Т.к. \angle EAD = \angle EBC \Rightarrow \angle EAD = \angle EBC = 180^{\circ} : 2 = 90^{\circ}.

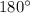В параллелограмме сумма односторонних углов равна 180^{\circ}.

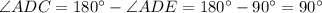
⇒ \angle ADC= 180^{\circ} - \angle ADE = 180^{\circ} - 90^{\circ} = 90^{\circ}

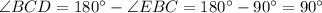
⇒ \angle BCD = 180^{\circ} - \angle EBC = 180^{\circ} - 90^{\circ} = 90^{\circ}

Параллелограмм, у которого все углы прямые - прямоугольник.


Впараллелограмме abcd точка e - середина стороны ab. известно, что ec = ed. докажите , что данный па
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
222вовчик222 222вовчик222  30.01.2021 22:08
1. Із вершини А гострого кута ромба ABCD, у якого АВ=ВD=2 см., проведено перпендикуляр АК до площини ромба так, що АК=1 см. Знайдіть довжину похилої КС. 2. Із вершини...
Alex96xelA Alex96xelA  30.01.2021 22:08
Твірна конуса дорівнює 4√3 см і нахилена до площини основи під кутом 30°. Через дві твірні конуса проведено площину під кутом 60° до площини основи. Знайдіть відстань...
2009tes 2009tes  30.01.2021 21:59
Знайдіть відстань від діагоналі АС грані куба АВСDA1B1C1D1 з ребром а до площини А1С1D1 ....
Mamiksem Mamiksem  30.01.2021 21:54
В параллелограмме ABCD AE - биссектриса угла А. Стороны параллелограмма AB и ВС относятся как 4:9. AE пересекает диагональ BD в точке К. Найтиотношение ВК :KD.Можно...
sabserj sabserj  30.01.2021 21:49
КТО ЗНАЕТ ГЕОМЕТРИЮ СЮДА Нужно найти: CBA с полным решением...
Lera2010K Lera2010K  22.09.2019 20:30
Сколько кубиков с ребром 5 см. можно отлить из шара радиус которого равен 10 см...
Bauer322 Bauer322  22.09.2019 20:30
Существует ли трицгольник со стр 1) 7 8 12 м 2) 4 3 8м...
Амишка51 Амишка51  22.09.2019 20:30
Сколько жемчужин потребуется для изготовления бус длиной 50 см, если радиус одной жемчужины равен 5 мм?...
chelsea6 chelsea6  02.12.2019 10:30
Ть будь ласка розв язати ! дано три вершини трикутника авс : а(3; -1), в(11; 3), с(-6; 2) знайдіть рівняння сторони ав...
ОлесяБычкова ОлесяБычкова  02.12.2019 10:29
Дано: треугольник абсpq || abap = pccq = qbs abc = 48 s apqb - ? ​...

Популярные вопросы