Восновании треугольной пирамиды лежит равнобедренный треугольник с основанием 34 дм и боковой стороной 32 дм. найдите высоту пирамиды, если боковые грани образуют с основанием двугранные углы 45 градусов.

Если все грани пирамиды находятся под одинаковым углом к основанию, значит вершина S пирамиды должна быть равноудалена от всех сторон основания пирамиды=> проекция точки S, точка O также должна быть равноудалена от всех сторон пирамиды, значит она находится в точке пересечения биссектрис углов треугольника который лежит в основании.

Допустим AB=BC=32 дм, тогда из точки B опустим высоту/биссектрису/медиану BH на основание AC, так как O∈BH и BH⊥AC=> по теореме о трех перпендикуляров SH будет ⊥ AC.

Угол OHS двугранный=45° по условию.

--------

Треугольник  SOH прямоугольный т.к. SO⊥плоскости(ABC)=>SO⊥OH.

так-же он равнобедренный так-как ∠OSH=180-90-45=45=∠SHO, значит высота SO=OH.

Задача свелась к простейшей планиметрической задаче по нахождению OH.

---------------------

сделаем вынос Треугольника ABC:

AO биссектриса, BH-медиана/высота.

По теореме пифагора:

Из свойств биссектрисы для треугольника ABH:

ответ: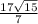

--------------

Если что-то непонятно задай вопрос.