1. Геометрия
  2. Во сколько раз уменьшится

Во сколько раз уменьшится V конуса, если диаметр его основания уменьшить в 2,5 раза? нужен не просто ответ, но и решение подробное ​

Mornes Mornes    3   27.06.2020 16:35    3

Ответы
Kikookiko Kikookiko  15.10.2020 15:00

Формула объёма конуса: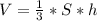 V = \frac{1}{3}*S*h , где

S - площадь основания

h - высота конуса

Т.к. основанием конуса является круг, то

Формула площади круга: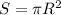 S = \pi R^{2} , где

π - число пи

R - радиус круга

Как мы знаем радиус - половина диаметра ⇒ формула может выглядеть и так: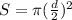  S = \pi (\frac{d}{2}) ^{2}

Получается формула объёма конуса становится такой: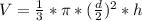  V = \frac{1}{3}*\pi *(\frac{d}{2} )^{2} *h

Теперь пусть d - диаметр нового конуса, тогда 2,5d - первоначальный диаметр конуса

V₁ - первоначальный объём конуса, а V₂ - новый объём конуса

Получается:

V_{1} = \frac{1}{3}*\pi *(\frac{2,5d}{2} )^{2} *h = \frac{1}{3}*\pi *(\frac{5d}{4} )^{2} *h = \frac{1}{3}*\pi *\frac{25d^{2}}{16} *h

V_{2} = \frac{1}{3}*\pi *(\frac{d}{2} )^{2} *h = \frac{1}{3}*\pi *\frac{d^{2} }{4} *h

Теперь ищем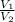 \frac{V_{1} }{V_{2} }

\frac{V_{1} }{V_{2} } = \frac{\frac{1}{3}*\pi *\frac{25d^{2}}{16} *h}{\frac{1}{3}*\pi *\frac{d^{2} }{4} *h}

\frac{1}{3},\pi и h сокращаются, получается:

\frac{V_{1} }{V_{2} } = \frac{\frac{25d^{2}}{16} }{ \frac{d^{2} }{4} } = \frac{25d^{2}}{16} : \frac{d^{2} }{4} = \frac{25d^{2}}{16} * \frac{4}{d^{2} } = \frac{25}{4} = 6 \frac{1}{4} = 6,25

ответ: в 6,25 раз уменьшится V конуса

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
ksenya64 ksenya64  01.06.2019 06:20
Придумайте на тему параллельность прямых + решить !...
missisvereshac missisvereshac  01.06.2019 06:20
Какая из данных фигур имеет только одну ось симметрии ? а)квадрат . б)окружность . в) парабола . г) отрезок...
serbinaluba66cet serbinaluba66cet  01.06.2019 06:20
Втреугольнике abc угол с равен 90 градусов. ac=8. bс=8√15 найдите радиус описанной окружености этого треугольника...
Айкотик2017 Айкотик2017  24.04.2020 08:35
Геометрия к/р, такое Дано: угол AOD = 90, угол OAD = 70, угол OCB = 20. Доказать: AD || BC. С решением по действиям...
phon1 phon1  24.04.2020 08:35
Какое из следующих утверждений верно?1) вертикальные углы равны. 2)две окружности пересекаются если радиус одной окружности больще радиуса другой окружности. 3)диагонали трапеции...
Шишеа Шишеа  24.04.2020 08:35
На рисунке дуга АС ровна 84(градуса).Чему равен угол ABC,опирающийся на эту дугу А)84(грдс)Б)42(грдс)В)незнаю И остальные задания тоже надо решить...
Germes11 Germes11  24.04.2020 08:34
ΔKLM — равнобедренный прямоугольный треугольник, около которого описана окружность; меньшая высота треугольника KO = 4,06 см. Найди: a) ∢ KML = °; б) OM = см; в) боковую сторону...
nastyaangel13 nastyaangel13  24.04.2020 08:34
**қай жануарды біржасушалылар тобына жатқызады? Олардың ортақ белгілерін ата. Қандай жануарды к деп атайды**​...
rkzxzvty2343 rkzxzvty2343  24.04.2020 08:34
В окружности с центром в точке O отрезки AC и BD - диаметры. Центральный угол AOD равен 76°. Найдите угол ACB. ответ дайте в градусах ​...
79654622969ss 79654622969ss  24.04.2020 08:34
Прямая AB касается окружности с центром в точке O радиуса r в точке B. Найдите AB если известно, что r=2 OA=2корень37​...

Популярные вопросы