Вгострокутному трикутнику авс проведені висоти аd ,be , cf . доведіть , що трикутник авс рівносторонній , якщо утворений чотирикутник fbde — ромб

По условию, FBDE - ромб ⇒ FB = BD = DE = FE и ∠DBE = ∠BFE.

Пусть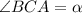 , BE - высота треугольника ABC и биссектриса острых углов ромба FBDE , то ΔABC - равнобедренный ⇒ ∠BAC = ∠BCA = α.

Отрезок АС виден под прямыми углами, следовательно, точки A, F, D, C лежат на окружности ⇒ DE - медиана и радиус окружности, следовательно, DE = EC  ⇒  ΔDEC - равнобедренный ⇒

∠EDC = ∠DCE = α. Тогда ∠DBE = 180° - α. Известно, что сумма углов четырехугольника равна 360°.

2∠FBD + 2∠DBE = 360°

2∠FBD + 360° - 2α = 360°

∠FBD = α

Таким образом, ∠A = ∠B = ∠C ⇒ ΔABC - равносторонний.