1. Геометрия
  2. Вцилиндр вписана правильная

Вцилиндр вписана правильная треугольная призма. площадь боковой поверхности призмы равна 5. найдите площадь боковой поверхности цилиндра.

llllsaaaaaa llllsaaaaaa    3   19.05.2019 01:10    0

Ответы
ololeg1 ololeg1  12.06.2020 06:37

Поскольку призма вписана в цилиндр то высоты обоих H одинаковы. Т. к. призма правильная, то площадь ее поверхности равна:
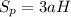
S_{p} = 3aH \\
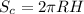
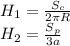
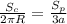
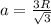
Далее площадь поверхности цилиндра равна:
S_{c} = 2 \pi RH
Поскольку у обоих одинаковые высоты, то мы можем приравнять их сначала выразив высоты обоих.:
H_{1} = \frac{S_{c}}{2 \pi R} \\ H_{2} = \frac{S_{p}}{3a}
Теперь приравняем их:
\frac{S_{c}}{2 \pi R} = \frac{S_{p}}{3a}
Далее для описанной окружности около треугольника (основая призмы) с радиусом R, длина стороны равна:
a = \frac{3R}{\sqrt{3}}
Теперь мы можем подставить это вместо "a" в нашем равенстве:

 \frac{S_{c}}{2 \pi R} = \frac{S_{p}}{3*\frac{3R}{\sqrt{3}}} \\ \frac{S_{c}}{2 \pi R} = \frac{S_{p}*\sqrt{3}}{9R} \\ \frac{S_{c}}{2 \pi R} = \frac{5\sqrt{3}}{9R} \\ \frac{S_{c}}{2 \pi} = \frac{5\sqrt{3}}{9} \\ S_{c} = \frac{10 \pi\sqrt{3}}{9}

Решал быстро, возможны ошибки :)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
viklap04 viklap04  16.12.2021 01:58
В треугольнике ABC уравнение биссектрисы угла A x-y-1=0, уравнение высоты из точки C x+3y-23=0 и B(6, 13). Найдите уравнение стороны AC...
daniilkeidi daniilkeidi  16.12.2021 01:44
Укажіть не правильну формулу (a+b)в квадраті=2ab+b в квадраті б)(a+b)квадраті=(a+b)квадраті•(a+b) в)(a+b)(а квадраті -аb+bквадраті=aКубі+bКубі г)(а+b)(b-а)=а квадраті...
Ochoba007 Ochoba007  16.12.2021 01:42
МОЛЮ , НИЧЕГО НЕ ПОНИМАЮ!(очень объяснение ещё)...
nikin25 nikin25  16.12.2021 01:40
ГЕОМЕТРИЯ 11 класс ИНТЕРНЕТУРОК! Три вектора заданы своими координатами: i (0;1;0) ; j (1;1;0) ; k (1;0;1) Разложите по этим векторам вектор f (9;7;4) Запишите полное...
velvis2050 velvis2050  16.12.2021 01:38
ГЕОМЕТРИЯ! Даны точки A(-3;2) и В(9;-3). Найдите координаты и длину векторов AB и BA. МНЕ НУЖНО С РАЗВЁРНУТЫМ ОТВЕТОМ...
nikitanosach2901 nikitanosach2901  16.12.2021 01:36
Найдите углы равнобокой трапеции, если ее боковая сторона 3 корень из 2, а диагональ, равная 3 корень из 3, образует с основанием угол 45 градусов...
YuliaVaskiv YuliaVaskiv  16.12.2021 01:25
До іть будь ласка! Діагональ основи правильної чотирикутної призми дорівнює 4√2 см, а висота 3см. Знайти об’єм призми. Диагональ основания правильной четырехугольной...
Лизотикенотик Лизотикенотик  27.07.2019 14:30
Во сколько раз внешний угол треугольника abc угол 1 меньше угла внутреннего 2...
dashabonya dashabonya  27.07.2019 14:30
3. периметр равнобедренного треугольника равен 45см, а одна из его сторон больше другой на 9см. найдите стороны треугольника....
moonlightbiebs13 moonlightbiebs13  17.08.2019 10:50
Разность смежных углов = 28 градусов найдите эти углы...

Популярные вопросы