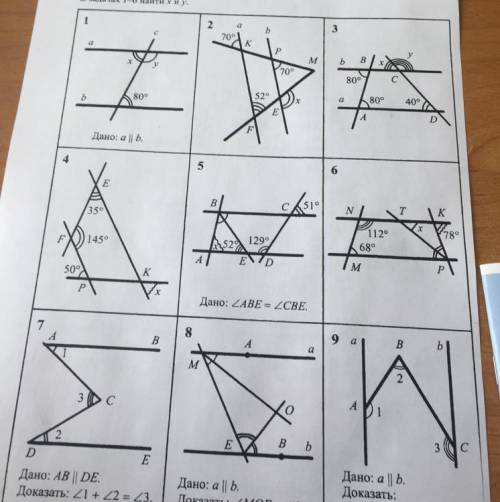
вас решить задачи (найти x и y) дам решите все)

Добрый день! Давайте рассмотрим задачу, которую вы предоставили. У нас есть система уравнений, в которой мы должны найти значения переменных x и y, чтобы они удовлетворяли обоим уравнениям.

Первым шагом мы можем сконцентрироваться на первом уравнении. Мы видим, что у нас есть сумма двух выражений, равная 10. Мы можем преобразовать это уравнение следующим образом:

2x + 3y = 10

Чтобы упростить это уравнение, мы можем избавиться от коэффициента 2, умножив оба выражения на 2:

4x + 6y = 20

Затем мы переходим ко второму уравнению:

y - x = -2

Мы можем переписать это уравнение следующим образом:

-y + x = 2

Теперь у нас есть система из двух уравнений:

4x + 6y = 20
-x + y = 2

Есть различные способы решения этой системы уравнений, но я покажу вам метод подстановки.

Давайте начнем с второго уравнения и разрешим его относительно одной переменной, чтобы затем подставить это значение в первое уравнение.

-x + y = 2

Разрешим его относительно x, прибавив x к обоим выражениям:

y = x + 2

Теперь мы можем взять это значение y и подставить его в первое уравнение:

4x + 6(y) = 20

4x + 6(x + 2) = 20

Распределяем 6 на оба выражения:

4x + 6x + 12 = 20

Складываем x и x:

10x + 12 = 20

Теперь мы хотим изолировать x, поэтому вычтем 12 из обоих выражений:

10x = 8

Делим оба выражения на 10:

x = 8/10

Мы можем упростить это дробное значение:

x = 4/5

Теперь, чтобы найти значение y, мы можем вернуться к уравнению y = x + 2 и подставить полученное значение x:

y = (4/5) + 2

y = (4/5) + (10/5)

y = 14/5

Итак, ответ: x = 4/5 и y = 14/5.

Мы нашли значения переменных x и y, которые удовлетворяют обоим уравнениям системы. Если у вас есть еще вопросы, пожалуйста, не стесняйтесь задавать!