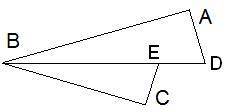
ВАС ОТ Дано, что BD — биссектриса угла CBA. BA⊥DAиCE⊥BC.
Найди BC, если DA= 9 см, BA= 12 см, CE= 6,3 см.
Сначала докажем подобие треугольников. (В каждое окошечко впиши одну латинскую букву или число.)
∢A=∢
=
°∢C
E=∢D
A,т.к.BE− биссектриса}⇒ΔBAD∼ΔBCE по двум углам (по первому признаку подобия треугольников).
BC=
см.
Другие вопросы по теме Геометрия
Популярные вопросы
- У рівнобедреному трикутнику основа дорівнює 8 см, а бісектриса проведена до основи...
3 - По источнику определите, кому были подчинены усуни: «Усуни долгое время находились...
3 - Выпеши глаголы где цыфра 2 определи ...
1 - 6 Вычисли.291 850 - (302.627 - 11704:56) , примеры надо решать по действиям, ...
3 - Топта өлеңді талдаңдар . Кестеге өлеңнен басқа топтың мүшелеріне түсін масалдар...
3 - Скільки цілих чисел містить множина розв‘язків система Решите,очень...
3 - решить 1) (6y-1)(y+2) (3y+4)(2y+1) 2) (3y-1)(2y+1) (2y-1)(2+3y)...
3 - ӨТІНЕМ КӨМЕКТЕСІНІЗДЕРШ КЕРЕК БОП ТУР...
3 - Измерение атмосферного давления. Опыт торричелли УПРАЖНЕНИНЯ на странице 131-132...
3 - . Укажите наименьшее целое решение неравенства: х+1/3-4х -7....
1
BD - это биссектриса угла CBA.
BA⊥DA - это означает, что отрезок BA перпендикулярен (пересекается под прямым углом) с отрезком DA.
CE⊥BC - это означает, что отрезок CE перпендикулярен отрезку BC.
Задача заключается в том, чтобы найти длину отрезка BC при известных длинах отрезков DA, BA и CE.
Перейдем к решению:
Сначала, мы можем заметить, что у нас есть два перпендикулярных треугольника - ΔBAD и ΔBCE. Нам нужно доказать, что эти треугольники подобны.
Для этого нам понадобятся два условия: угол-угол-угол (УУУ) и угол-угол-сторона (УУС).
Угол-угол-угол:
∠A = ∠C, потому что BD является биссектрисой угла CBA (это означает, что он делит угол на две равные части, поэтому углы A и C равны).
∠E = ∠D, потому что BE является биссектрисой угла CBE (это означает, что он делит угол на две равные части, поэтому углы E и D равны).
Угол-угол-сторона:
∠B = ∠B (одинаковые углы)
Таким образом, по первому признаку подобия треугольников (УУУ или УУС) мы можем сказать, что ΔBAD подобен ΔBCE.
Теперь, когда мы знаем, что эти треугольники подобны, мы можем использовать соотношение между сторонами подобных треугольников:
AB/BD = DA/CE
Подставим известные значения:
12/BD = 9/6.3
Теперь найдем BD:
BD = (12 * 6.3)/9
BD = 84/9
BD = 9.33 см
Теперь используем найденное значение BD для нахождения BC:
BD/BC = DA/CE
9.33/BC = 9/6.3
Подставим известные значения:
9.33/BC = 1.35
Теперь найдем BC:
BC = 9.33/1.35
BC ≈ 6.9 см
Таким образом, длина отрезка BC составляет примерно 6.9 см.