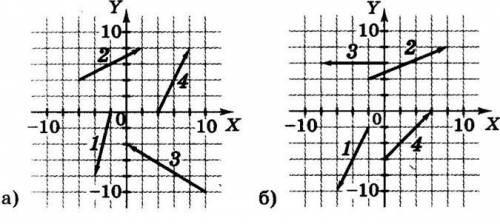
В задании нужно выписать координаты вектора и записать разложение вектора по координатным векторам ради бога, умоляю...

Добрый день!

Для начала, давай разберемся, что такое вектор и координаты вектора. Вектор - это направленный отрезок, который имеет длину (модуль) и направление. Вектор часто обозначают строчной латинской буквой с надчеркиванием, например, в данном случае обозначим его как AB̅.

Координаты вектора - это числа, которые показывают его положение относительно заданной системы координат. В данном задании у нас есть система координат с осями OX и OY. Обычно координаты вектора записывают в виде (x, y), где x - координата по оси OX, а y - координата по оси OY.

Теперь перейдем к заданию. Нам нужно выписать координаты вектора AB̅ и записать его разложение по координатным векторам. Для этого мы должны определить начальную и конечную точки вектора, а затем найти разность координат конечной и начальной точек.

Итак, посмотрим на данное изображение. У нас есть точка A с координатами (0, 0) и точка B с координатами (3, 2).

1. Выписывание координат вектора AB̅:
Для этого мы просто вычисляем разность координат конечной и начальной точек:
Координата x вектора AB̅ = x координаты точки B - x координаты точки A = 3 - 0 = 3.
Координата y вектора AB̅ = y координаты точки B - y координаты точки A = 2 - 0 = 2.
Таким образом, координаты вектора AB̅ равны (3, 2).

2. Разложение вектора AB̅ по координатным векторам:
Для этого мы должны разложить вектор AB̅ на сумму векторов, параллельных осям координат.
В нашем случае, это будут два вектора: вектор по оси OX и вектор по оси OY.

Вектор по оси OX: Это вектор, у которого координата y равна 0.
То есть, он направлен только вдоль оси OX, а его координата y равна 0.
Разложение вектора AB̅ по вектору по оси OX будет иметь вид: (3, 0).

Вектор по оси OY: Это вектор, у которого координата x равна 0.
То есть, он направлен только вдоль оси OY, а его координата x равна 0.
Разложение вектора AB̅ по вектору по оси OY будет иметь вид: (0, 2).

Таким образом, разложение вектора AB̅ по координатным векторам будет иметь вид: (3, 0) + (0, 2).

Надеюсь, что данное объяснение было понятным и полезным для тебя! Если у тебя остались какие-либо вопросы, не стесняйся задавать их. Я всегда готов помочь!