1. Геометрия
  2. В треугольнике MNK MN =

В треугольнике MNK MN = NK = 18 см, MK = 12 см, NE
биссектриса треугольника. Найдите отрезок MЕ.

rustam05mirzaev rustam05mirzaev    3   18.11.2020 20:36    12

Ответы
mahachkala1 mahachkala1  18.12.2020 20:45

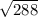
ME = \sqrt{288}

Объяснение:

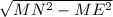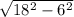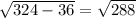Треугольник MNK - равнобедренный(MN = NK по условию), тогда по свойству равнобедренного треугольника биссектриса опущенная на основание является медианой и высотой следовательно ME = EK = MK / 2 = 12 / 2 = 6.NE перпендикулярно MK так как NE - высота. Тогда треугольник MEN прямоугольный и по теореме Пифагора ME = \sqrt{MN^{2}-ME^{2} } = \sqrt{18^{2}-6^{2} } = \sqrt{324 - 36} = \sqrt{288}.


В треугольнике MNK MN = NK = 18 см, MK = 12 см, NE биссектриса треугольника. Найдите отрезок MЕ.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
ИльяФеоктистов ИльяФеоктистов  18.05.2019 22:50
Впрямоугольнике периметр равен 52 см,а его стороны относятся как 4: 9. а)найдите площадь прямоугольника. б)найдите сторону квадрата,площадь которого равна площади прямоугольника....
светлана498 светлана498  18.05.2019 22:50
Найдите обьем правильной четырехугольной пирамиды у которой боковое ребро = 2корень с 2 см а апофема = корень с 6...
kenzhegali1 kenzhegali1  18.05.2019 22:50
Вравнобедренной трапеции основания относятся как 1: 3, диагональ равна 42 см. середина одной из боковых сторон и конец большего основания, не принадлежащий этой стороне, соединены...
Fezit Fezit  18.05.2019 22:50
Может ли в равнобедренном треугольнике основание равное боковой стороне?...
57Nika57 57Nika57  18.05.2019 22:50
Втреугольнике авс, ав=4см ас=7см угол а=30 градусов. найти: а)площадь треугольника. б)высоту, проведенную к стороне ав....
6469678 6469678  18.05.2019 22:50
Вравнобедренном треугольнике боковая сторона равна 24 см. через середину высоты, опущенной на его основание, проведена прямая, параллельная боковой стороне, до пересечения с двумя...
nikitasolyny nikitasolyny  18.05.2019 22:50
Надо! ! в треугольнике abc сн-высота, ad-биссектриса, о-точка пересечения прямых ch и ad,угол bad равен 74 градуса.найдите угол аос.ответ дайте в градусах...
Егорка156 Егорка156  18.05.2019 22:50
Диагональ ромба равна его стороне, длина которой 6см. найдите вторую диагональ и углы ромба....
Профессионал228 Профессионал228  14.09.2019 00:30
Как перевести обыкновенную дробь в десятичную....
vovaonuchko vovaonuchko  14.09.2019 00:30
Вкруге отметили точку. разрежьте круг на две части и сложите из них новый круг, чтобы отмеченная точка попала в его центр. точка может быть где угодно в круге, но не в центре. нужно...

Популярные вопросы