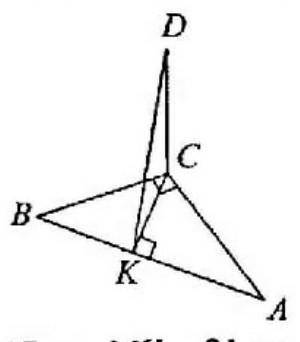
В треугольнике АВС из вершины прямого угла С к стороне АВ проведена высота СК. ВС - 30 см, АС = 40 см. Из вершины С к плоскости треугольника АВС проведен перпендикуляр CD. Найдите расстояние оточки D до плоскости треугольника АВС, если расстояние от точки D до гипотенузы АВ равно 40 см

АБ=72
СК=27
АС=36
Я не вижу смысла нет мне писать на этот адрес электронной почты и не только в этом случае не оплаты и копии документов по почте или по телефону говорит что не

Для решения этой задачи нам потребуется использовать свойства треугольников и понятие расстояния от точки до плоскости.

Дано:
В треугольнике АВС из вершины прямого угла С к стороне АВ проведена высота СК. ВС = 30 см, АС = 40 см. Из вершины С к плоскости треугольника АВС проведен перпендикуляр CD. Расстояние от точки D до гипотенузы АВ равно 40 см.

Задача:
Найти расстояние от точки D до плоскости треугольника АВС.

Решение:
1. Для начала обратимся к свойству высоты треугольника. Если из вершины прямого угла С опущена перпендикулярная прямая к стороне АВ, то она является высотой. Обозначим точку пересечения высоты СК с гипотенузой как М.
2. Теперь нам нужно найти значение расстояния МК. Заметим, что треугольник АСК является подобным треугольнику АВС (по свойству высоты, выделенного участка гипотенузы и затененной области). Поэтому отношение стороны МК к стороне МС будет равно отношению стороны АК к стороне АС. АК известно равным 40 см, АС равно 40 см, поэтому МК = 40 см.
3. Вспомним, что расстояние от точки D до гипотенузы АВ равно 40 см. Обозначим это расстояние как Х.
4. Заметим, что треугольник СМК также является подобным треугольнику САД, так как у них угол МСК и угол АдС перпендикулярны, и угол СКМ и угол САД прямые. Поэтому отношение стороны МК к стороне СК будет равно отношению стороны Х к стороне АС. МК мы уже нашли равным 40 см, АС равно 40 см, поэтому Х/40 = 40/30.
5. Перемножим средние члены пропорции и решим уравнение: Х * 30 = 40 * 40. Получим Х = 53,33 см.
6. Таким образом, расстояние от точки D до плоскости треугольника АВС равно 53,33 см.

Ответ: Расстояние от точки D до плоскости треугольника АВС равно 53,33 см.